简介
基本概念及原理
一种表述:Embedding 是个英文术语,如果非要找一个中文翻译对照的话,我觉得“向量化”(Vectorize)最合适。Embedding 的过程,就是把数据集合映射到向量空间,进而把数据进行向量化的过程。Embedding 的目标,就是找到一组合适的向量,来刻画现有的数据集合。
- 比如让国家作为模型参数,我们该如何用数字化的方式来表示它们呢?毕竟,模型只能消费数值,不能直接消费字符串。一种方法是把字符串转换为连续的整数,然后让模型去消费这些整数。。在理论上,这么做没有任何问题。但从模型的效果出发,整数的表达方式并不合理。为什么这么说呢?我们知道,连续整数之间,是存在比较关系的,比如 1 < 3,6 > 5,等等。但是原始的字符串之间,比如,国家并不存在大小关系,如果强行用 0 表示“中国”、用 1 表示“美国”,逻辑上就会出现“中国”<“美国”的悖论。仅仅是把字符串转换为数字,转换得到的数值是不能直接喂给模型做训练。
- 我们需要把这些数字进一步向量化,才能交给模型去消费。Embedding 的方法也是日新月异、层出不穷。从最基本的热独编码到 PCA 降维,从 Word2Vec 到 Item2Vec,从矩阵分解到基于深度学习的协同过滤,可谓百花齐放、百家争鸣。
一种表述:embedding 是指将客观世界中离散的物体或对象(如单词、短语、图片)等映射到特征空间的操作,embedding向量是指映射后 的特征空间中连续且稠密的高维向量。在机器学习场景中,我们经常使用embedding向量 来描述客观世界的物体。embedding向量 不是对物体进行简单编号的结果,而是在尽量保持相似不变性的前提下 对物体进行特征抽象和编码的产物。通过不断训练,我们能够将客观世界中的物体不失真的映射到高维特征空间中,进而可以使用这些embedding向量 实现分类、回归和预测等操作。
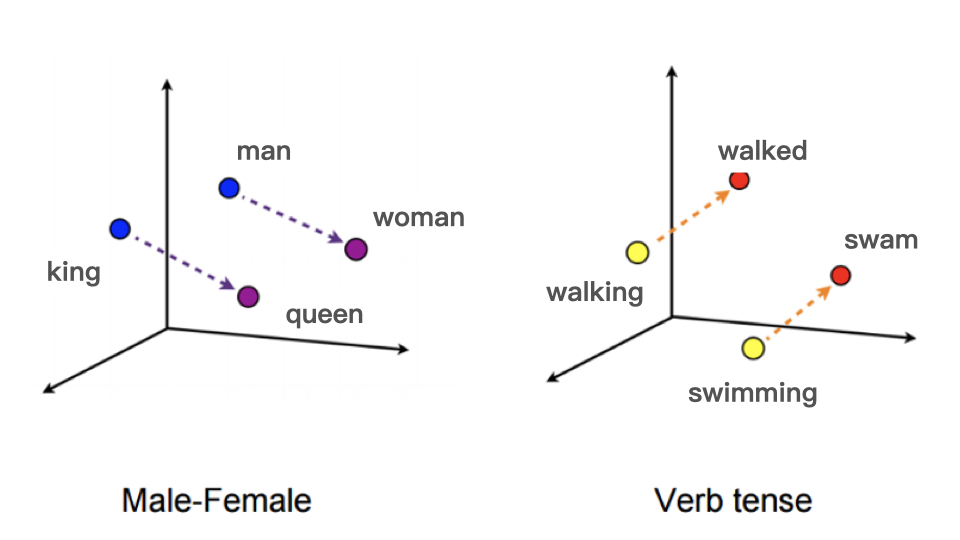
Embedding 就是用一个数值向量“表示”一个对象(Object)的方法。“实体对象”可以是image、word等,“数值化表示”就是一个编码向量。例如对“颜色“这种实体对象用(R,G,B)这样一个三元素向量编码。embedding还可以理解成将离散目标投影到连续空间中的某个点上。数值化的embedding vector本身是没有意义的,不同vector之间的相对关系才是有实际意义的。例如:NLP中最基本的word embedding,给每一个单词一个N维编码向量(或者说将每个word投影到N维空间中),我们期望这种编码满足这样的特性:两个向量之间的”距离“越小,代表这两个单词含义越接近。比如利用 Word2vec 这个模型把单词映射到了高维空间中,从 king 到 queen 的向量和从 man 到 woman 的向量,无论从方向还是尺度来说它们都异常接近。
Embedding 技术对深度学习推荐系统的重要性
- Embedding 是处理稀疏特征的利器。因为推荐场景中的类别、ID 型特征非常多,大量使用 One-hot 编码会导致样本特征向量极度稀疏,而深度学习的结构特点又不利于稀疏特征向量的处理,因此几乎所有深度学习推荐模型都会由 Embedding 层负责将稀疏高维特征向量转换成稠密低维特征向量。
- Embedding 可以融合大量有价值信息,本身就是极其重要的特征向量 。 相比由原始信息直接处理得来的特征向量,Embedding 的表达能力更强,特别是 Graph Embedding 技术被提出后,Embedding 几乎可以引入任何信息进行编码,使其本身就包含大量有价值的信息,所以通过预训练得到的 Embedding 向量本身就是极其重要的特征向量。
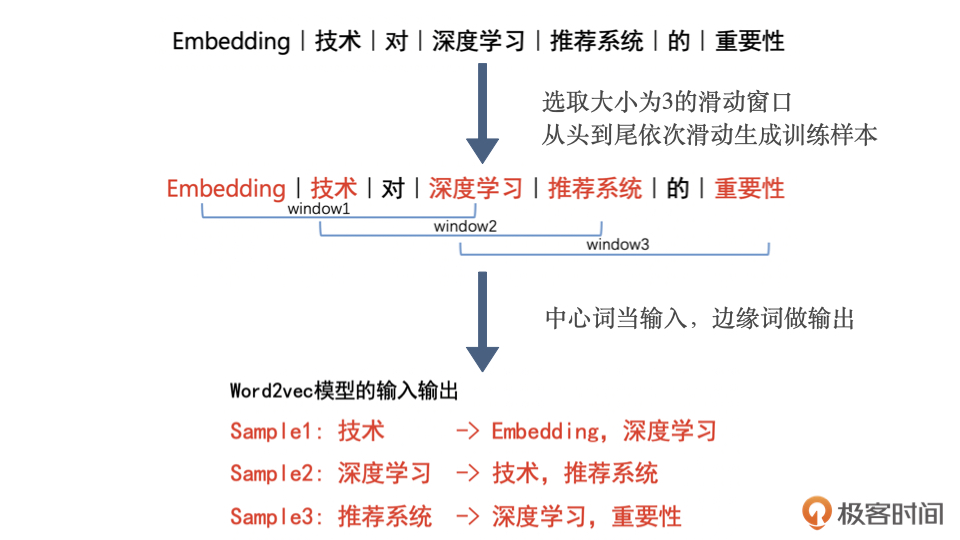
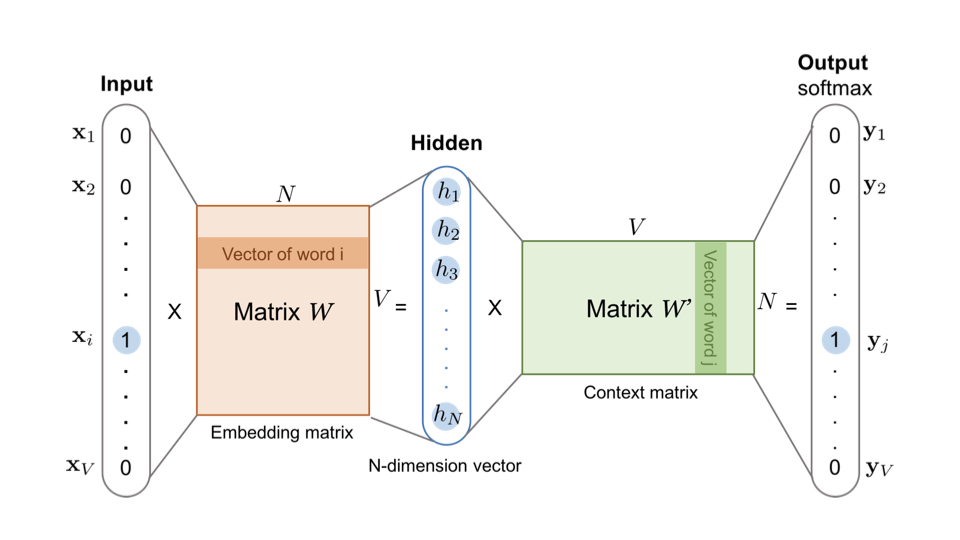
Word2vec 是生成对“词”的向量表达的模型,其中,Word2vec 的训练样本是通过滑动窗口一一截取词组生成的。在训练完成后,模型输入向量矩阵的行向量,就是我们要提取的词向量。
在 Word2vec 诞生之后,Embedding 的思想迅速从自然语言处理领域扩散到几乎所有机器学习领域,既然 Word2vec 可以对词“序列”中的词进行 Embedding,那么对于用户购买“序列”中的一个商品,用户观看“序列”中的一个电影,也应该存在相应的 Embedding 方法。于是,微软于 2015 年提出了 Item2Vec 方法,它是对 Word2vec 方法的推广,使 Embedding 方法适用于几乎所有的序列数据。只要能够用序列数据的形式把我们要表达的对象表示出来,再把序列数据“喂”给 Word2vec 模型,我们就能够得到任意物品的 Embedding 了。假设我们知道 用户看过的电影的id 序列,比如296 380 344 588 593 231 595 318 480,那么此时电影id 是词,电影id 序列是句子,一个句子内的词有相互关系,那么就可以 根据 Item2vec 计算电影id 对应的 Embedding 向量。
Embedding这块,spark MLlib 和 机器学习库 都提供了处理函数。利用Tensorboard很容易将embedding进行可视化,不过既然是可视化,最高只能“可视”三维空间,所以高维向量需要被投影到三维(或二维空间)。不过不用担心细节,Tensorboard做了足够高质量的封装。
- 端到端的方法是将Embedding层作为神经网络的一部分,在进行BP更新每一层参数的时候同时更新Embedding,这种方法的好处是让Embedding的训练成为一个有监督的方式,可以很好的与最终的目标产生联系,使得Embedding与最终目标处于同一意义空间。但这样做的缺点同样显而易见的,由于Embedding层输入向量的维度甚大,Embedding层的加入会拖慢整个神经网络的收敛速度。大部分的训练时间和计算开销都被Embedding层所占据。正因为这个原因,「对于那些时间要求较为苛刻的场景,Embedding最好采用非端到端,也就是预训练的方式完成。」
- 非端到端(预训练),在一些时间要求比较高的场景下,Embedding的训练往往独立于深度学习网络进行,在得到稀疏特征的稠密表达之后,再与其他特征一起输入神经网络进行训练。在做任务时,将训练集中的词替换成事先训练好的向量表示放到网络中。Word2Vec,Doc2Vec,Item2Vec都是典型的非端到端的方法
在自然语言中,非端到端很常见,因为学到一个好的的词向量表示,就能很好地挖掘出词之间的潜在关系,那么在其他语料训练集和自然语言任务中,也能很好地表征这些词的内在联系,预训练的方式得到的Embedding并不会对最终的任务和模型造成太大影响,但却能够「提高效率节省时间」,这也是预训练的一大好处。但是在推荐场景下,根据不同目标构造出的序列不同,那么训练得到的Embedding挖掘出的关联信息也不同。所以,「在推荐中要想用预训练的方式,必须保证Embedding的预训练和最终任务目标处于同一意义空间」,否则就会造成预训练得到Embedding的意义和最终目标完全不一致。比如做召回阶段的深度模型的目标是衡量两个商品之间的相似性,但是CTR做的是预测用户点击商品的概率,初始化一个不相关的 Embedding 会给模型带来更大的负担,更慢地收敛。
在梯度下降这块对embedding weight也有针对性的优化算法,从梯度下降到FTRLFTRL是在广告/推荐领域会用到的优化方法,适用于对高维稀疏模型进行训练,获取稀疏解。
实践
《深度学习推荐系统实战》为什么深度学习的结构特点不利于稀疏特征向量的处理呢?一方面,如果我们深入到神经网络的梯度下降学习过程就会发现,特征过于稀疏会导致整个网络的收敛非常慢,因为每一个样本的学习只有极少数的权重会得到更新,这在样本数量有限的情况下会导致模型不收敛。另一个方面,One-hot 类稀疏特征的维度往往非常地大,可能会达到千万甚至亿的级别,如果直接连接进入深度学习网络,那整个模型的参数数量会非常庞大。因此,我们往往会先通过 Embedding 把原始稀疏特征稠密化,然后再输入复杂的深度学习网络进行训练,这相当于把原始特征向量跟上层复杂深度学习网络做一个隔离。
案例
从论文源码学习 之 embedding_lookup Embedding最重要的属性是:越“相似”的实体,Embedding之间的距离越小。比如用one-hot编码来表示4个梁山好汉。
李逵 [0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0]
刘唐 [0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
武松 [0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
鲁智深 [0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
==>
二 出 官 武
货 家 阶 力
李逵 [1 0 0 0.5]
刘唐 [1 0 0 0.4]
武松 [0 1 0.5 0.8]
鲁智深 [0 1 0.75 0.8]
Embedding层把我们的稀疏矩阵,通过一些线性变换(比如用全连接层进行转换,也称为查表操作),变成了一个密集矩阵,这个密集矩阵用了N(例子中N=4)个特征来表征所有的好汉。在这个密集矩阵中,表象上代表着密集矩阵跟单个好汉的一一对应关系,实际上还蕴含了大量的好汉与好汉之间的内在关系(如:我们得出的李逵跟刘唐的关系)。它们之间的关系,用嵌入层学习来的参数进行表征。这个从稀疏矩阵到密集矩阵的过程,叫做embedding,很多人也把它叫做查表,因为它们之间也是一个一一映射的关系。这种映射关系在反向传播的过程中一直在更新。因此能在多次epoch后,使得这个关系变成相对成熟,即:正确的表达整个语义以及各个语句之间的关系。这个成熟的关系,就是embedding层的所有权重参数。Embedding最大的劣势是无法解释每个维度的含义,这也是复杂机器学习模型的通病。
Embedding除了把独立向量联系起来之外,还有两个作用:降维,升维。
- embedding层 降维的原理就是矩阵乘法。比如一个 1 x 4 的矩阵,乘以一个 4 x 3 的矩阵,得倒一个 1 x 3 的矩阵。4 x 3 的矩阵缩小了 1 / 4。假如我们有一个100W X 10W的矩阵,用它乘上一个10W X 20的矩阵,我们可以把它降到100W X 20,瞬间量级降了。
- 升维可以理解为:前面有一幅图画,你离远了看不清楚,离近了看就可以看清楚细节。当对低维的数据进行升维时,可能把一些其他特征给放大了,或者把笼统的特征给分开了。同时这个embedding是一直在学习在优化的,就使得整个拉近拉远的过程慢慢形成一个良好的观察点。
如何生成?
- 矩阵分解
- 无监督建模
- 有监督建模
Embedding与深度学习推荐系统的结合
NVIDIA HugeCTR,GPU版本参数服务器— (5) 嵌入式hash表 具有两个嵌入表和多个全连接层的神经网络
Embedding 权重矩阵可以是一个 [item_size, embedding_size] 的稠密矩阵,item_size是需要embedding的物品个数,embedding_size是映射的向量长度,或者说矩阵的大小是:特征数量 * 嵌入维度。Embedding 权重矩阵的每一行对应输入的一个维度特征(one-hot之后的维度)。用户可以用一个index表示选择了哪个特征。
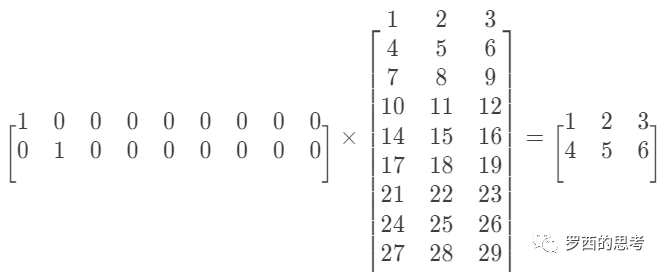
这样就把两个 1 x 9 的高维度,离散,稀疏向量,压缩到 两个 1 x 3 的低维稠密向量。这里把 One-Hot 向量中 “1”的位置叫做sparseID,就是一个编号。这个独热向量和嵌入表的矩阵乘法就等于利用sparseID进行的一次查表过程。
TensorFlow 的 embedding_lookup(params, ids) 函数的目的是按照ids从params这个矩阵中拿向量(行),所以ids就是这个矩阵索引(行号),需要int类型。即按照ids顺序返回params中的第ids行。比如说,ids=[1,3,2],就是返回params中第1,3,2行。返回结果为由params的1,3,2行组成的tensor。
embedding_lookup是一种特殊的全连接层的实现方法,其针对 输入是超高维 one hot向量的情况。
- 神经网络处理不了onehot编码,Z = WX + b。由于X是One-Hot Encoding 的原因,WX 的矩阵乘法看起来就像是取了Weights矩阵中对应的一行,看起来就像是在查表,所以叫做 lookup。
embedding_lookup(W,X)等于说进行了一次矩阵相乘运算,其实就是一次线性变换。 - 假设embedding权重矩阵是一个
[vocab_size, embed_size]的稠密矩阵W,vocab_size是需要embed的所有item的个数(比如:所有词的个数,所有商品的个数),embed_size是映射后的向量长度。所谓embedding_lookup(W, id1),可以想像成一个只在id1位为1的[1, vocab_size]的one_hot向量,与[vocab_size, embed_size]的W矩阵相乘,结果是一个[1, embed_size]的向量,它就是id1对应的embedding向量,实际上就是W矩阵的第id1行。但是,以上过程只是forward,因为W一般是随机初始化的,是待优化的变量。因此,embedding_lookup除了要完成以上矩阵相乘的过程(实现成“抽取id对应的行”),还要完成自动求导,以实现对W的更新。PS: 所以embedding_lookup 的底层是一个op,在tensorflow r1.4 分支下,底层执行的是array_ops.gather
tensorflow 实现
一般在tensorflow中都会使用一个shape=[id_index_size, embedding_size]的Variable 矩阵做embedding参数,然后根据id特征的index去Variable矩阵中查表得到相应的embedding表示。这里需要注意的是:id_index_size的大小一般都不会等于对应id table的元素个数,因为有很多id元素不在原始的id table表中,比如新上架的一些商品等。此时需要将id_index_size设置的大一些,以留一些位置给那些不在id table表的元素使用。
使用tf.Variable 作为 embedding参数
import numpy as np
import tensorflow as tf
sess = tf.InteractiveSession()
embedding = tf.Variable(np.identity(6, dtype=np.int32)) # 创建一个embedding词典
input_ids = tf.placeholder(dtype=tf.int32, shape=[None])
# 相对于 feature_column 中的EmbeddingColumn,embedding_lookup 是有点偏底层的api/op
input_embedding = tf.nn.embedding_lookup(embedding, input_ids) # 把input_ids中给出的tensor表现成embedding中的形式
sess.run(tf.global_variables_initializer())
print("====== the embedding ====== ")
print(sess.run(embedding) )
print("====== the input_embedding ====== ")
print(sess.run(input_embedding, feed_dict={input_ids: [4, 0, 2]}))
====== the embedding ======
[[1 0 0 0 0 0]
[0 1 0 0 0 0]
[0 0 1 0 0 0]
[0 0 0 1 0 0]
[0 0 0 0 1 0]
[0 0 0 0 0 1]]
====== the input_embedding ======
[[0 0 0 0 1 0]
[1 0 0 0 0 0]
[0 0 1 0 0 0]]
使用get_embedding_variable接口
var = tf.get_embedding_variable("var_0",embedding_dim=3,initializer=tf.ones_initializer(tf.float32),partitioner=tf.fixed_size_partitioner(num_shards=4))
shape = [var1.total_count() for var1 in var]
emb = tf.nn.embedding_lookup(var, tf.cast([0,1,2,5,6,7], tf.int64))
...
使用categorical_column_with_embedding接口
columns = tf.feature_column.categorical_column_with_embedding("col_emb", dtype=tf.dtypes.int64)
W = tf.feature_column.embedding_column(categorical_column=columns,dimension=3,initializer=tf.ones_initializer(tf.dtypes.float32))
ids={}
ids["col_emb"] = tf.SparseTensor(indices=[[0,0],[1,1],[2,2],[3,3],[4,4]], values=tf.cast([1,2,3,4,5], tf.dtypes.int64), dense_shape=[5, 4])
emb = tf.feature_column.input_layer(ids, [W])
从论文源码学习 之 embedding层如何自动更新input_embedding = embedding * input_ids 从效果上 可以把 input_ids 视为索引的作用,返回第4、0、2 行数据,但 embedding_lookup 函数 也可以看做是一个 矩阵乘法(底层两种都支持,是一个策略参数),也因此 embedding层可以通过 optimizer 进行更新。
原生的tf optimizer 根据 梯度/grad 的类型 来决定更新weight/ variable 的方法,当传来的梯度是普通tensor时,调用_apply_dense方法去更新参数;当传来的梯度是IndexedSlices类型时,则去调用optimizer._apply_sparse_duplicate_indices函数。 Embedding 参数的梯度中包含每个 tensor 中发生变化的数据切片 IndexedSlices。IndexedSlices类型是一种可以存储稀疏矩阵的数据结构,只需要存储对应的行号和相应的值即可。可以认为是一种类似 SparseTensor 的思想,用元素数据和元素位置表示一个较大 tensor 。将 tensor 按第一维度切片,从而将一个较大的形状为 [LARGE0, D1, .. , DN] 的 tensor 表示为多个较小的形状为 [D1, .. , DN] 的 tensor。
总结一下涉及到哪些问题: 稀疏参数的表示(开始由Variable 表示 ,各种框架提供EmbeddingVariable 表示)、存储(ps,底层是分布式hashmap)、通信(只通信部分,数据存在gpu + gpu 直接通信)、优化(稀疏参数的优化器与稠密参数的优化器不兼容) 和 稀疏参数的梯度的表示、通信(由IndexedSlices 表示)、优化
嵌入层的优化
DL 推荐模型的嵌入层是比较特殊的:它们为模型贡献了大量参数,但几乎不需要计算,而计算密集型denser layers的参数数量则要少得多。所以对于推荐系统,嵌入层的优化十分重要。
原理上
TensorFlow在美团外卖推荐场景的GPU训练优化实践-参数规模的合理化
- 去交叉特征
- 精简特征
- 压缩Embedding向量数
- 压缩Embedding向量维度
- 量化压缩
工程上
embedding部分的难点在于存储和检索。DNN这部分主要是稠密计算。Embedding 优化
- 把嵌入层分布在多个 GPU 和多个节点上
- Embedding 层模型并行,dense 层数据并行。