简介(持续更新)
从数学的知识体系出发,一直到具体的编程应用,整个过程本身是一个很长的链条:数学概念 - 数学模型 - 数据结构 - 基础算法 / 机器机器学习算法 - 编码实现
为什么学数学
数学理论和编程实践的结合其实是“决裂”的,所以学习数学的时候,你不能太功利,觉得今天学完明天就能用得着,我觉得这个学习思路可以用在其他课程上,但放在数学里绝对不合适。
徐文浩:理解“程序”和“问题的解决方案”的关系。大部分应用领域的核心解决方案,都是把应用领域的问题,形式化为一个个数学问题。在找到数学问题的“解法”之后,用写程序的方式翻译成实际应用的“算法”。而能够应用“数学”的方式来解决问题,是从一个只能套用现成方案的“码农”,向能够将新问题形式化、并找出创新解决方案的“研发工程师”迈出的第一步。
之前没那么火,但早早就在搜索、广告这些领域,应用的机器学习和推荐算法。这里面其实就是结合了微积分、线性代数、概率论之后的最优化问题。
王天一:作为非数学专业出身的“外行”,我们使用数学的目的不是顶天,而是立地;不是上下求索艰深的理论问题,而是将生活中的具体问题抽象化,进而加以解决。因此,对于我们这些票友来说,学习数学的基础在于经验而非哲学,比较实际的思路是秉持功利主义的原则,用多少学多少。掌握基本的线性代数与矩阵论、概率论与数理统计知识足以应付日常的使用,盲目地好高骛远通常有害无益。理论化和公理化这些比较深邃的尝试固然让人着迷,但它们可能并没有肉眼可见的实用性,对于绝大部分计算机从业者恐怕过于阳春白雪。PS:不要死钻定理,用好也是本事。
其次,在学习时还要理解数学的本质。数学是工具而非问题,是手段而非目的。探索世界奥秘的学科是“格物穷理”的物理学,相形之下,数学更像是个任人打扮的小姑娘,它存在的意义就是通过合理的设计简化物理学的研究。正因如此,在数学中存在着各种各样在现实中不可能出现的理想化模型(比如无穷小和极限的诞生),也存在着对同一个物理过程不同的建模方式(比如矩阵力学和波动力学)。充分理解数学的人造特质,可以在学习中少走很多无谓的弯路。
理解数学的工具属性就会自然而然地引出了数学学习中的另一个关键点,那就是工具设计的出发点,也就是所谓的数学思想与数学逻辑。任何一个工具都不是平白无故地设计出来的,它必然要解决某个特定的问题,比如线性代数与矩阵论是对具体对象的抽象表示与运算,比如概率论和数理统计是对不确定性及其定性定量表示的建模。因此,在掌握每一种数学工具的微观技巧之前,理解它们的宏观目标是更加重要的。只有掌握了工具诞生的背景与目的,才有可能有效地使用它们。如何透过现象看本质,将不同场景融会贯通,才是值得锻炼的高级能力。PS:认知的几点规律学习这个东西,没有什么捷径。而且往往是需要先明白更多抽象的相对比较难的东西之后,学习简单的东西就只是一个查文档的过程。
数学 ==> 人造 ==> 工具 ==> 发明工具的初衷 ==> 透过现象看本质(相同问题的不同方法,不同问题的相同方法) ==> 融会贯通
学什么?
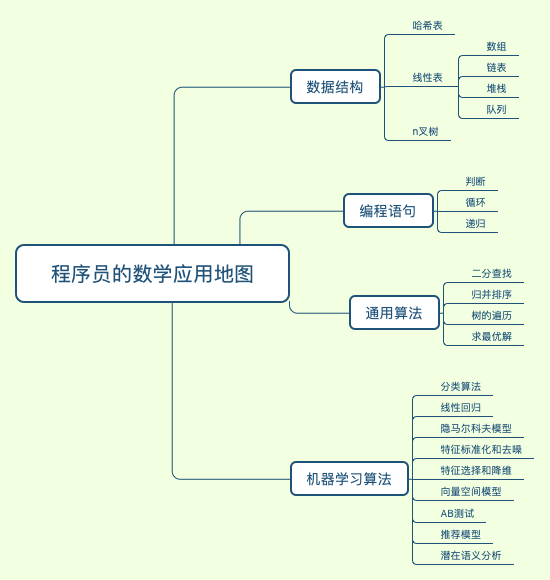
计算机使用二进制和现代计算机系统的硬件实现有关,由于每位数据只有断开与接通两种状态,所以即便系统受到一定程度干扰时,它仍然能够可靠地分辨出数字是“0”还是“1”。二进制的数据表达具有抗干扰能力强、可靠性高的优点。另外,二进制也非常适合逻辑运算。逻辑运算中的“真”和“假”,正好与二进制的“0”和“1”两个数字相对应。
求余 ==> 哈希:将任意长度的输入,通过哈希算法,压缩为某一固定长度的输出
数学归纳法与递归
数学归纳法:对于某些迭代问题,我们其实可以避免一步步的计算,直接从理论上证明某个结论,节约大量的计算资源和时间
将数学归纳法的思想泛化成更一般的情况?数学归纳法考虑了两种情况:
- 初始状态,也就是 n=1 的时候,命题是否成立;
- 如果 n=k-1 的时候,命题成立。那么只要证明 n=k 的时候,命题也成立。其中 k 为大于 1 的自然数。
将上述两点顺序更换一下,再抽象化一下,我写出了这样的递推关系
- 假设 n=k-1 的时候,问题已经解决(或者已经找到解)。
- 那么只要求解 n=k 的时候,问题如何解决(或者解是多少);初始状态,就是 n=1 的时候,问题如何解决(或者解是多少)
比如归并排序,就是假设两个子数组是有序的,那么n=k时,排序问题变成了两个子有序数组如何合并。PS:将问题进行了转化,这是数学归纳法的价值所在。
假设有四种面额的钱币,1 元、2 元、5 元和 10 元,要找零给顾客10元,有多少种方式?
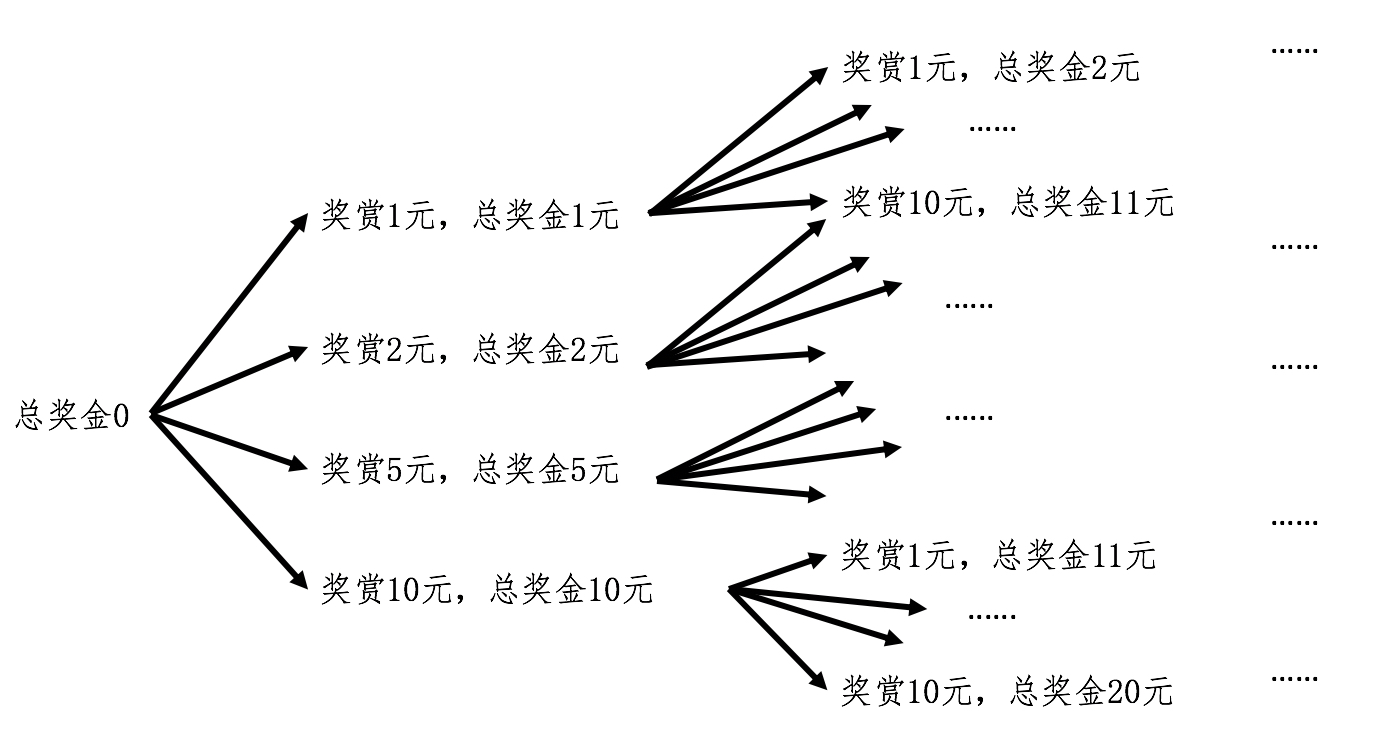
虽然迭代法的思想是可行的,但是如果用循环来实现,恐怕要保存好多中间状态及其对应的变量。在递归中,每次嵌套调用都会让函数体生成自己的局部变量,正好可以用来保存不同状态下的数值,为我们省去了大量中间变量的操作,极大地方便了设计和编程。PS:是否可以从递推是广度优先,递推是深度优先来考虑问题呢?
叫排列组合 还是叫 组合排列
组合是指从 n 个不同元素中取出 m(1≤m≤n)个不同的元素。从 n 个不同的元素中取出 m(1≤m≤n)个不同的元素,按照一定的顺序排成一列,这个过程就叫排列。从这个视角来说叫组合排列更顺一点,但组合数的求解用到了排列,所以通常叫排列组合。
排列其实是一个树状结构,在概率中,排列有很大的作用,因为排列会帮助我们列举出随机变量取值的所有可能性,用于生成这个变量的概率分布。此外,排列在计算机领域中有着很多应用场景,最多的是穷举法,比如密码的暴力破解。
组合适合找到多个元素之间的联系而并不在意它们之间的先后顺序,例如多元文法中的多元组(不管用户输入的单词是什么顺序,都将其转换为特定顺序,然后按特定顺序查询)
矩阵
- 向量在不同学科眼里是不同的东西,甚至于它可以是任何东西,只要保证其相加和数乘有意义即可。为什么只需要相加和数乘,只需要这2种运算,就可以到达空间内的任何一点。
- 函数是将一个输入经过一些处理变为一个输出,如y=f(x)。那向量的运算a=L(b)也是如此,为什么我们不把向量的运算叫函数,而都是叫向量变换/矩阵变换呢?这提醒我们要用运动的思想看待向量的计算,或者换一种说法,矩阵/向量变换是对空间的变换。矩阵变化都是线性变换(因为都是依赖向量数乘和相加):原点不动;直线依然是直线。
- 矩阵是对一个空间的变换:一个向量 左乘一个矩阵得到的值的几何意义是:这个向量在新的空间(经过矩阵变换后的空间)里的位置。

在含有一个隐层的感知机中, Z = WX + B Z 可以看做是X经过 线性变换W后的表示,Z 和 X 都表示输入的特征,只是维度不同。
数学
离散数学 主要分为数论和图论
概率论研究的就是这些概率之间相互转化的关系,比如联合概率、条件概率和边缘概率。
概率研究的是模型如何产生数据,统计研究的是如何通过数据来推导其背后的模型。
如果我们把每种结果的概率看作权重,那么期望值就是所有结果的加权平均值。
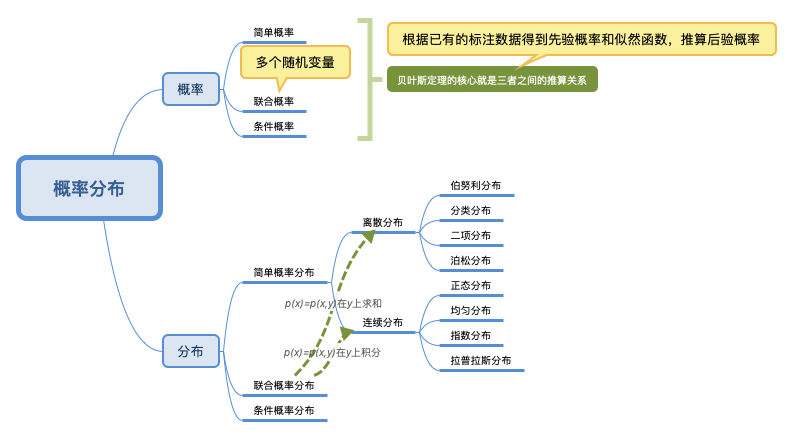
学习这些概念是为了做什么呢?其实就是为了更精确地描述我们生活中的现象,用数学的视角看世界,以此解决其中的问题。
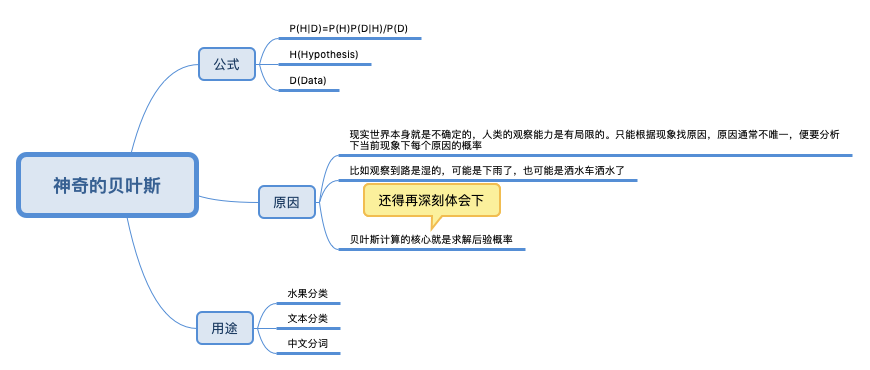
刘未鹏《暗时间》:所谓的贝叶斯方法源于他生前为解决一个“逆概”问题写的一篇文章。 在这篇文章之前,人们已经能够计算”正向概率“,如“一个袋子N个白球M个黑球,你伸手进去摸一把,摸出黑球的概率多大”。而一个自然而然的问题反过来:如果事先不知道袋子中黑白球比例,而是闭着眼睛摸出好几个球,观察这些取出来的球的颜色之后,那么我们可以对袋子中黑白球的比例做出怎样的推测?贝叶斯是机器学习的核心方法之一, 这背后的深刻原因在于:现实世界本身就是不确定的,人类的观察能力是有局限的,设想我们要是能直接观察到电子的运行, 还需要对原子模型争吵不休么?
分类算法 ==> 给事物定性的艺术
这个公式看着没什么感觉,但在贝叶斯分类中就很有用武之地了。比如我们将水果的形状、颜色、纹理、重量、握感、口感全部数值化。可以得到一个苹果、橙子是黄颜色的概率分别是多少,基于贝叶斯公式就可以反推一个黄色的、圆形水果是苹果、橙子的概率。前者是训练数据,后者是计算机根据贝叶斯分类算法做出的判断。因为计算机只能存储和计算可以数据化的东西,它无法知道一个水果是啥,但通过传感器可以知道一个水果的甜度、形状和颜色。
文本分类:如何区分特定类型的新闻?每个单词可以作为文章的属性,而通过这些单词的词频(出现的频率),我们很容易进行概率的统计。PS:这里笔者最有感触的就是“每个单词可以作为文章的属性”,就好比形状、颜色 可以作为一个水果的属性一样。