简介
建议看下前文 《数据结构与算法之美》——数据结构笔记
思考的过程比结论更重要。
\[\sum(Z)\]字符串匹配
先将主串拆分为 n-m+1 个子串,然后模式串与子串一一匹配
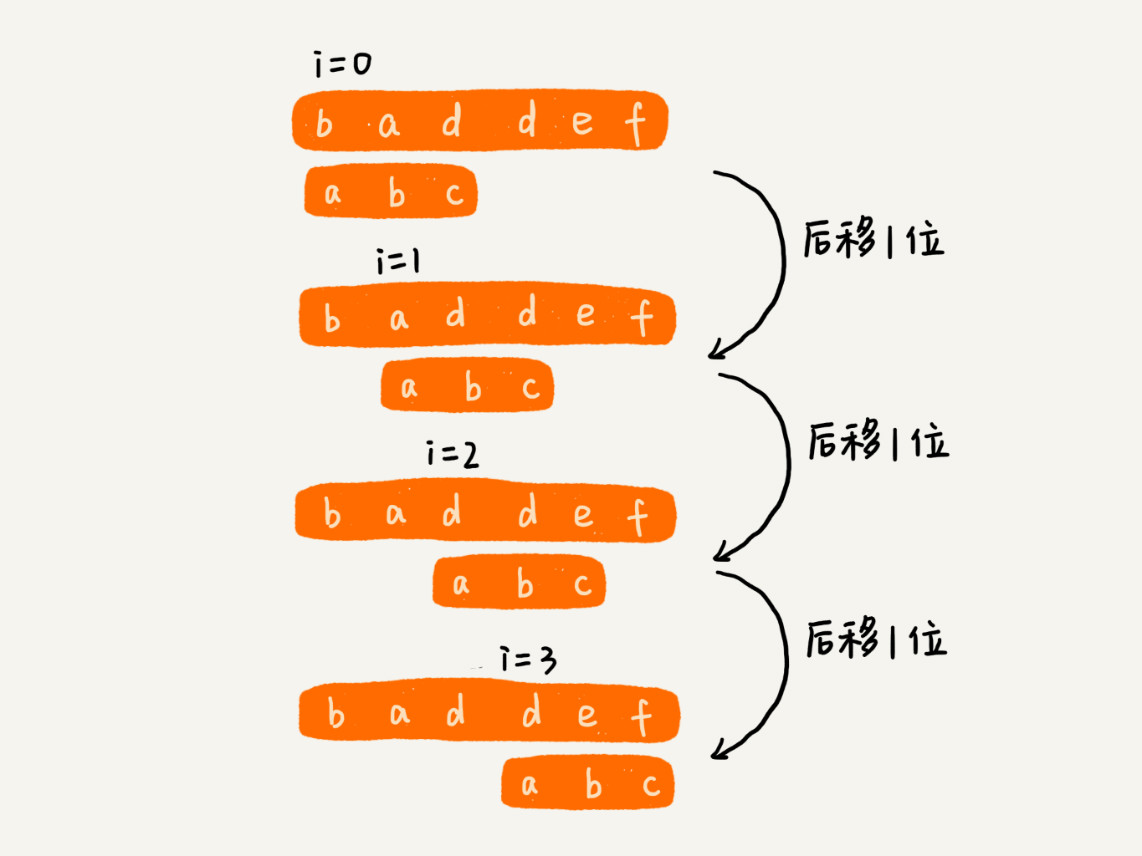
模式串与字串的匹配方式
- Brute Force 算法:暴力匹配
- Rabin-Karp 算法,在匹配效率(快速判断两个字符串是否相等 ==> 哈希 ==> 如何快速求哈希)上做文章
- Boyer-Moore 算法,常用于文本编辑器中的查找替换。当遇到不匹配的字符时,有什么固定的规律,跳过一些肯定不会匹配的情况,将模式串往后多滑动几位呢?BM 算法构建的规则有两类:坏字符规则和好后缀规则。好后缀规则可以独立于坏字符规则(耗内存、某些场景下失效)使用
-
Knuth Morris Pratt/KMP 算法,当遇到不匹配的字符时,将模式串往后多滑动几位呢?好前缀规则。 这里有两个事情:模式串(长度为n)有n-1个好前缀;每个前缀有它自己的后移位数

Rabin-Karp 算法
- 先全部算一遍哈希值,哈希值匹配
- 前一个字串与后一个字串的哈希值计算有关联关系, 省去部分计算
针对a~z组成的字符串 设计一个哈希算法,将其转换为一个数字
- 字符串对应一个26进制数字,数字可能很大, 计算机表示不了
- a~z 对应1~26,将所有字母对应的数字求和,容易冲突
- a~z 对应素数(这就引出了素数的价值),这样求和时冲突的概率就很低了
Trie树
字符串的匹配问题,笼统上讲,其实就是数据的查找问题。Trie 树的本质,就是利用字符串之间的公共前缀,将重复的前缀合并在一起。
如何存储一个 Trie 树?假设我们的字符串中只有从 a 到 z 这 26 个小写字母
-
散列表方式
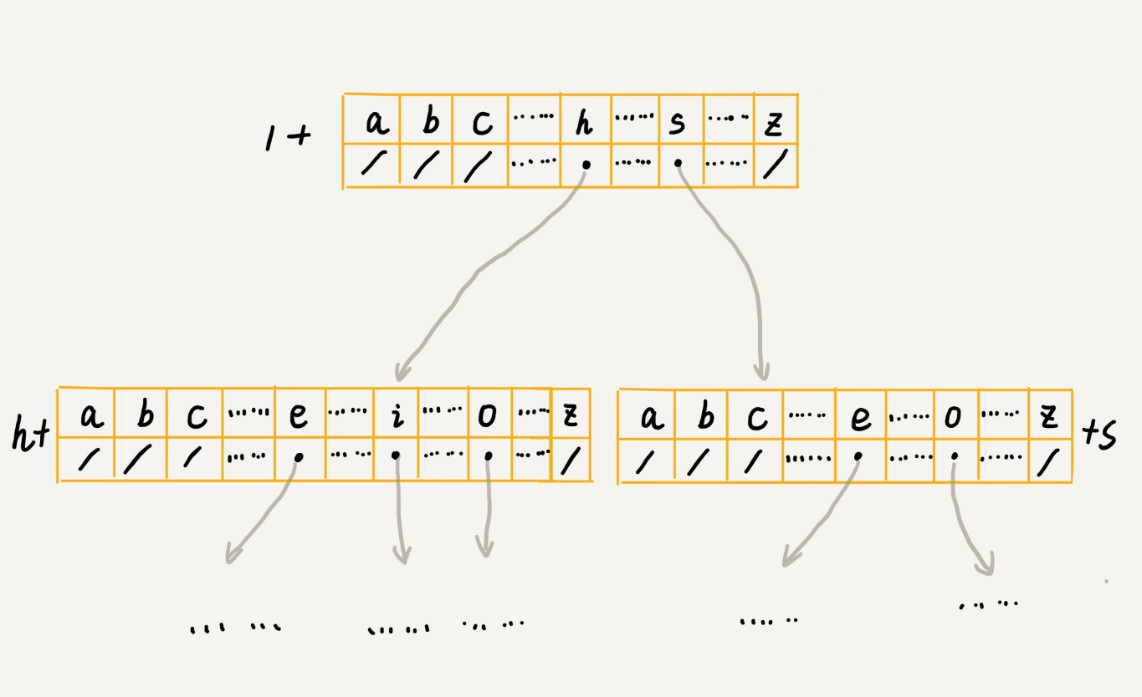
class TrieNode { char data; TrieNode children[26]; } -
每个节点中的数组换成其他数据结构,来存储一个节点的子节点指针。用哪种数据结构呢?我们的选择其实有很多,比如有序数组、跳表、散列表、红黑树等。假设我们用有序数组,数组中的指针按照所指向的子节点中的字符的大小顺序排列。查询的时候,我们可以通过二分查找的方法,快速查找到某个字符应该匹配的子节点的指针。但是,在往 Trie 树中插入一个字符串的时候,我们为了维护数组中数据的有序性,就会稍微慢了点。
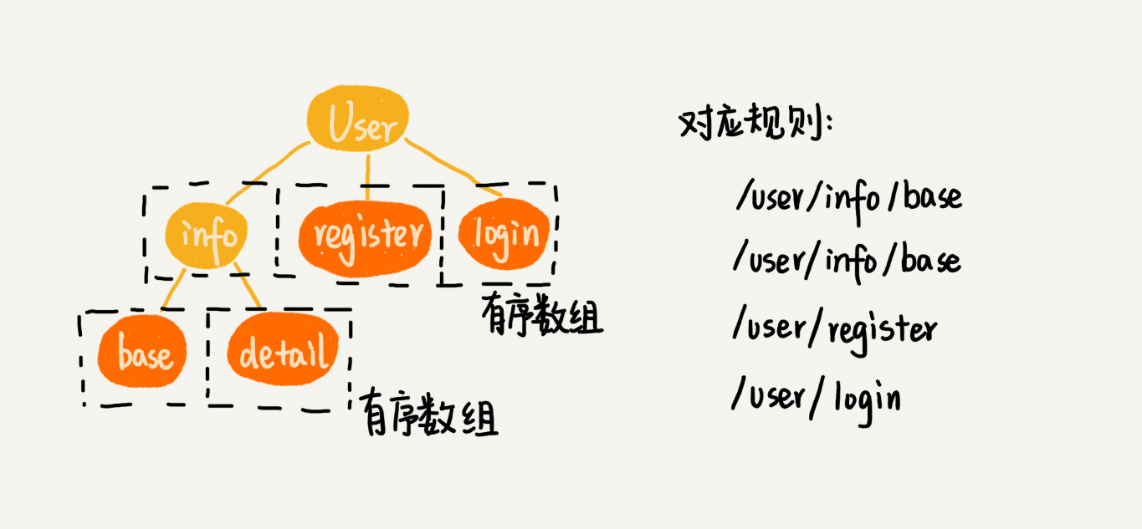
Trie 树不适合精确匹配查找,这种问题更适合用散列表或者红黑树来解决。Trie 树比较适合的是查找前缀匹配的字符串
trie 在路径匹配上的妙用(nginx或网关上经常用到),充分体现了:运用之妙,存乎一心。招式常变,思想永存。
多模式匹配
多模式串匹配算法,就是在多个模式串和一个主串之间做匹配,也就是说,在一个主串中查找多个模式串。比如很多网站提供敏感词过滤功能,也就是通过维护一个敏感词的字典,当用户输入一段文字内容之后,通过字符串匹配算法,来查找用户输入的这段文字,是否包含敏感词。如果敏感词很多,比如几千个,单模式处理思路比较低效。多模式匹配算法 只需要扫描一遍主串,就能在主串中一次性查找多个模式串是否存在
- 对敏感词字典进行预处理,构建成 Trie 树
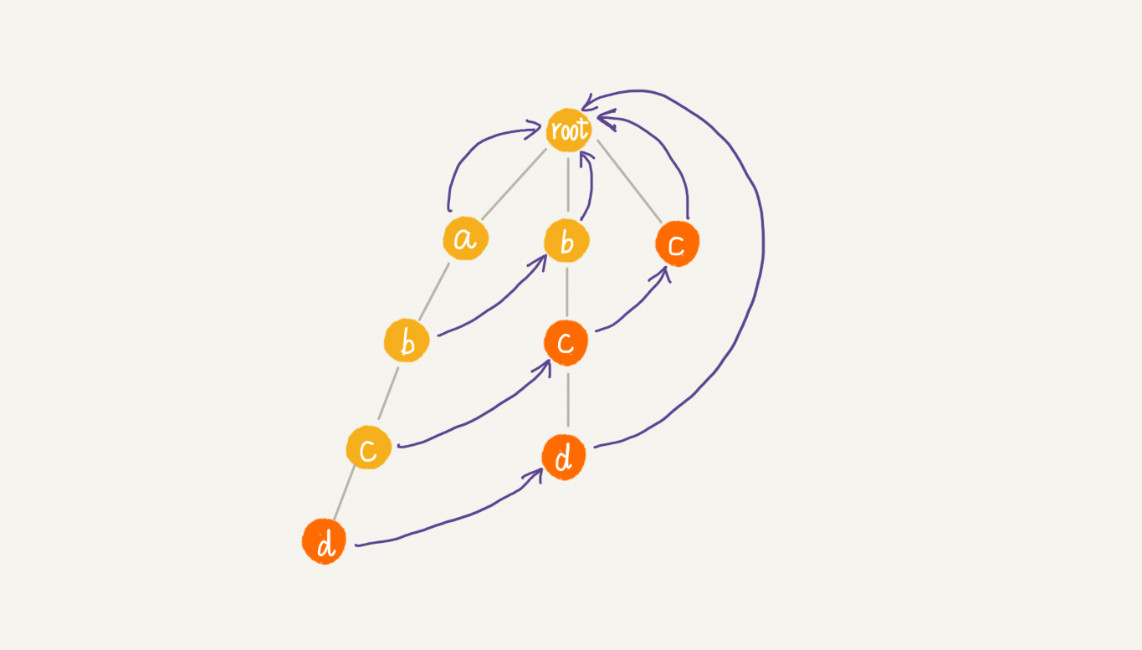
- 当用户输入一个文本内容后,我们把用户输入的内容作为主串,从第一个字符(假设是字符 C)开始,在 Trie 树中匹配。当匹配到 Trie 树的叶子节点,或者中途遇到不匹配字符的时候,我们将主串的开始匹配位置后移一位,也就是从字符 C 的下一个字符开始,重新在 Trie 树中匹配。这有点类似单模式串匹配的 BF 算法
- 我们知道,单模式串匹配算法中,KMP 算法对 BF 算法进行改进,引入了 next 数组,让匹配失败时,尽可能将模式串往后多滑动几位。借鉴单模式串的优化改进方法,有一个AC自动机算法。
public class AcNode {
public char data;
public AcNode[] children = new AcNode[26]; // 字符集只包含 a~z 这 26 个字符
public boolean isEndingChar = false; // 结尾字符为 true
public int length = -1; // 当 isEndingChar=true 时,记录模式串长度
public AcNode fail; // 失败指针,相当于 KMP 中的失效函数 next 数组
public AcNode(char data) {
this.data = data;
}
}
算法思想
从算法思想的角度来理解具体算法。
分治
分治与递归的关系:分治算法是一种处理问题的思想,递归是一种编程技巧,分治算法一般都比较适合用递归来实现
分治算法能解决的问题,一般需要满足下面这几个条件:
- 原问题与分解成的小问题具有相同的模式;
- 原问题分解成的子问题可以独立求解,子问题之间没有相关性(划分算法的选择标准),这一点是分治算法跟动态规划的明显区别。
- 具有分解终止条件,也就是说,当问题足够小时,可以直接求解;
- 可以将子问题合并成原问题,而这个合并操作的复杂度不能太高,否则就起不到减小算法总体复杂度的效果了。PS:所以分治算法为什么比常规最笨的算法高效?分治算法的复杂性=PartA+PartB+union(A,B),PartA和PartB的复杂性与笨方法并无区别,比笨方法优化就优化在对AB合并逻辑的处理上。
分治算法思想的应用是非常广泛的,并不仅限于指导编程和算法设计。利用这种分治的处理思路,不仅仅能克服内存的限制,还能利用多线程或者多机处理,加快处理的速度。
多阶段决策最优解——贪心、回溯和动态规划
贪心算法最难的一块是如何将要解决的问题抽象成贪心算法模型,然后才可以定义什么叫“贪心”。贪心算法适用的场景比较有限(假设一个决策分3步,可能除了第一步是最优的其它都是最差的)。这种算法思想更多的是指导设计基础算法。
回溯算法本质上就是枚举,非常适合用递归代码实现,优点在于其类似于摸着石头过河的查找策略,且可以通过剪枝少走冤枉路。它可能适合应用于缺乏规律,或我们还不了解其规律的搜索场景中。
我们假定一个基本判断:算法是一步一步优化得来的。 那么以回溯法的枚举为起点,除了剪枝外(比如不得超过背包总重量),还有哪些优化方式?类似于字符串匹配的算法演化过程:当遇到不匹配的字符时,有什么固定的规律,跳过一些肯定不会匹配的情况,将模式串往后多滑动几位呢?
考虑回溯法两个基本步骤:向下搜索和向上回溯。
- 向下搜索优化。类似于字符串匹配算法的演化,KMP提了一个next数组,next数组本质是模式串某种特征的表示,使得模式串向后滑动时可以一次性滑动多位。所以向下搜索时,是否可以发掘问题的特征,直接否定某些分支的可能性?PS: 贪心算法只向下,不搜索
- 向上回溯优化。如果对一个路径不满意要回头,是否可以不要回到root上,而是回到某个节点再向下搜索?所以一个优化点是回溯 + “备忘录”,每次回头回到上一步即可。
以这个为思维背景,来看下动态规划问题的三个特征
- 最优子结构,可以通过子问题的最优解,推导出问题的最优解。PS:贪心算法要求通过局部最优的选择,能产生全局的最优选择。一个是推导,一个是直接产生。
- 无后效性,暂未找到一个通俗的解释
- 重复子问题,不同的决策序列,到达某个相同的阶段时,可能会产生重复的状态。PS:这是分治算法不允许的。
可以看到
- 基于最优子结构规律,可以向下搜索优化,某些分支直接放弃
- 基于重复子问题,可以使用备忘录记录子问题的节,向上回溯优化。
假设我们有一个 n 乘以 n 的矩阵 w[n][n]。矩阵存储的都是正整数。棋子起始位置在左上角,终止位置在右下角。我们将棋子从左上角移动到右下角。每次只能向右或者向下移动一位。从左上角到右下角,会有很多不同的路径可以走。我们把每条路径经过的数字加起来看作路径的长度。那从左上角移动到右下角的最短路径长度是多少呢?
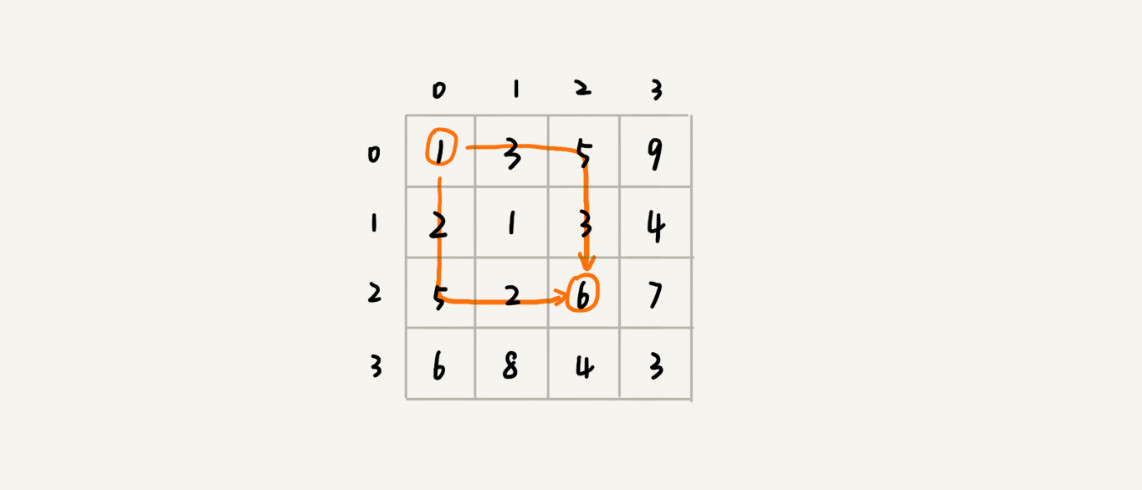
如果我们走到 (i, j) 这个位置,我们只能通过 (i-1, j),(i, j-1) 这两个位置移动过来
- 也就是说,我们想要计算 (i, j) 位置对应的状态,只需要关心 (i-1, j),(i, j-1) 两个位置对应的状态
- 也就是说,这是一个二叉树
我们把从起始位置 (0, 0) 到 (i, j) 的最小路径,记作 min_dist(i, j),记作 min_dist(i, j),可以得到状态转移方程(别名;子问题之间的转移关系)
min_dist(i, j) = w[i][j] + min(min_dist(i, j-1), min_dist(i-1, j))
对应上文
- min_dist(i, j) 作为备忘录,记录子问题的解,向上回溯优化
- min(min_dist(i, j-1), min_dist(i-1, j)) 体现了问题规律,向下搜索优化
个人感觉:有了状态转移方程,动态规划 从一个编程问题转换为了一个编程递推问题,代码中连递归都用不上了。
捋捋关系
图和和树都有深度优先和广度优先遍历算法, 而很多问题都可以建模为树和图,所以你不仅要把问题的存储建模为树和图,还要将问题的解决过程建模为深度或广度遍历。树和图都有最优化问题,而最优化问题 求解的过程 类似一个树。从下文两位大牛的回答可以看到,动态规划和Dijkstra 都是广度遍历的推广,A*搜索算法又是对Dijkstra的优化。由此可以看到 很多问题都可以建模为树和图(存储部分),解决过程可以建模为BFS或DFS,或者是对BFS或DFS的变种。如果再考虑广度优先和队列的关系、深度优先和栈的关系,感觉算法都是一家人。
戴克斯特拉算法(Dijkstra)的本质是贪心,还是动态规划? - 大雄的回答 - 知乎
贪心是一种特殊的动态规划,动态规划的本质是独立的子问题,而贪心则是每次可以找到最优的独立子问题。贪心和动归不是互斥的,而是包含的,贪心更快,但约束更强,适应范围更小。
动归和bfs的关系也是一样的。展开一点讲,在求解最优化问题时,有多个解。而求解的过程类似一个树,我们称之为求解树。一般的求解树真的是一棵树,所以我们只能用bfs来搜索,顶多剪枝。有些特殊的求解树,中间很多结点是重合的,结点个数比所有搜索分支的个数少很多个数量级。这类问题较特殊,我们可以保存中间的搜索过程。而记忆化搜索和动态规划本质上就是一个东西,快就快在可以不用重复计算很多中间结果(所谓的最优子问题)。
还有一些特殊的求解树,更特殊,它们不止有很多重复结点,而且每次选择分支的时候,我们可以证明只要选择一个分支,这个分支的解就一定比其他选择更优。这类问题就是贪心了。
所以bfs,dp,贪心三个方法都是解决最优化问题的方法,根据问题的不同,约束越大的问题可以用越快的方法,越慢的方法可以解决的问题越普适。
戴克斯特拉算法(Dijkstra)的本质是贪心,还是动态规划? - Sanho的回答 - 知乎
在边权全是 1 的图上,我们可以用 BFS 求单源最短路。Dijkstra 是 BFS 的推广。
捋一下算法之间的关系很重要,很多时候看到一个算法很神奇,那肯定是还没有理解透,肯定很快会忘记。认知是分层的,如果你知道优化路径,“来龙去脉”,有助于减少认知和思维负担。知识一开始是孤岛,然后联系起来形成一个网,最后共性的东西向上聚合,形成一个锥形。

从上图的优化步骤可以看到,优化思路是有章可循的:那就是尽可能利用问题本身的特点,找到暴力算法中的无效部分,并排除它。
再谈递归
刚接触递归的时候,大多数初学者脑子很容易跟着机器执行的顺序往深里绕,就像 Debug 一个很深的函数调用链一样,每遇到一个函数就 step into,也就是递归函数展开 -> 下一层 -> 递归函数展开 -> 下一层 ->…,结果就是只有“递”,没有“归”,大脑连一次完整调用的一半都跑不完(或者跑完一次很辛苦),自然就会觉得无法分析。
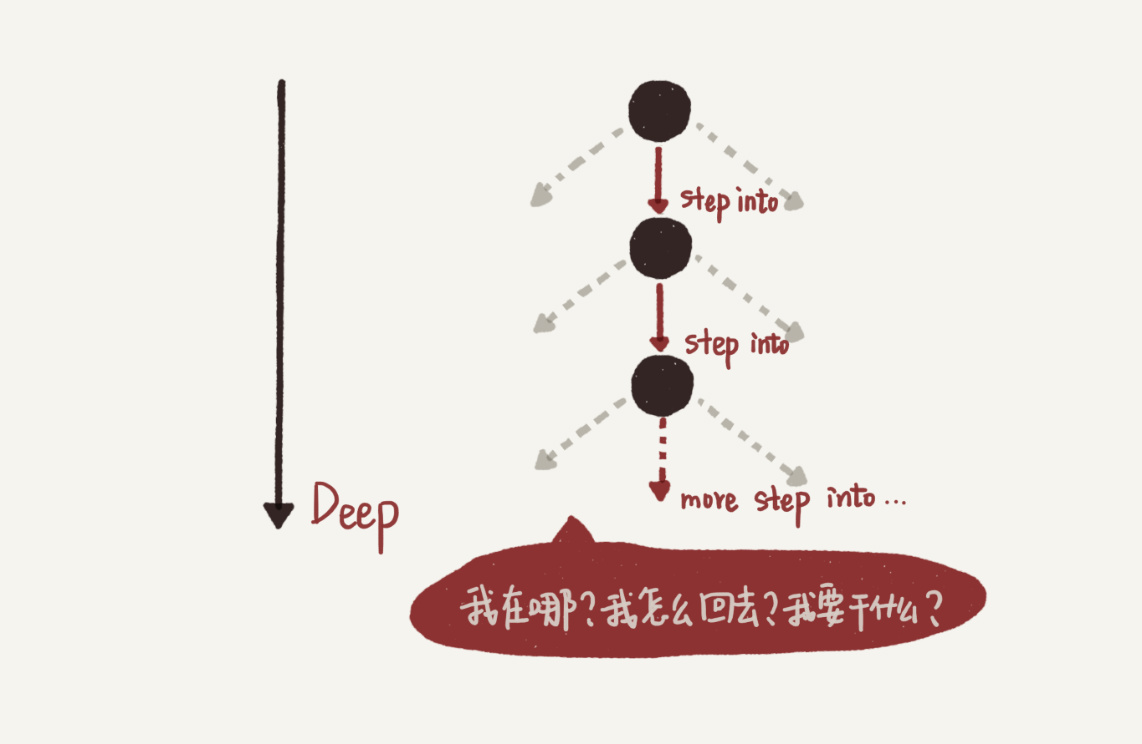
为什么人的思考一定要 follow 机器的执行呢?不管在哪一层,都是在执行递归函数这同一份代码,不同的层只有一些状态数据不同而已,所以只需要保证递归函数代码逻辑的正确性,就确保了运行时任意一层的结果正确性。在递归函数体中,不用每遇到递归调用都展开并进入下一一层(step into),而是可以直接假定下一层调用能够正确返回,然后该干嘛就继续干嘛(step over),只需要保证最深一层的逻辑,也就是递归的终止条件正确即可。PS:其数学原理是数学归纳法,参见《程序员的数学基础课》笔记
在实现一个递归函数的时候,其实就是在确定这棵树的整体形状:什么时候终止,什么条件下生出子树,也就是说实际上是在编程实现一棵树。递归的执行过程,就是在这棵树上做深度遍历的过程,每次进入下一层(“递”)就是压栈,每次退出当前层(“归”)就是出栈。
在用树解决问题时,有时树的叶子节点表示一个解,有时从root到叶子节点的路径(先序、中序、后序遍历)表示一个解,有时一层表示一个解的状态(比如分治),有时整体/部分表示一个解(最大堆和最小堆)。
什么样的编程方式可以实现树节点和边的操作(遍历、查询)?递归。但我希望大家换个方式来理解这个逻辑链条:按照最笨的编程方法去操作树,发现需要下探和回溯,用到了栈。把函数的嵌套调用,看作访问下一个连通的结点;把函数的返回,看作没有更多新的结点需要访问,回溯到上一个结点。 递归可以看做是这种通用逻辑的抽象、语法糖 想起另一句话:数据结构其实就是一个个解决问题的“模型”。有了这些模型,你就能把一个个具体的问题抽象化,然后再来解决。
计算机系统里的函数递归,在内部也是通过栈来实现的。虽然直接通过栈来实现递归不如函数递归调用那么直观,但是,由于栈可以避免过多的中间变量,它可以节省内存空间的使用。全面异步化:淘宝反应式架构升级探索 异步化会将操作系统中的队列情况显式地提升到了应用层。栈代替递归也可说是将 os的栈外化到 代码层。
高级篇
- 拓扑排序:凡是需要通过局部顺序来推导全局顺序的,一般都能用拓扑排序来解决。
- 最短路径与地图路线规划,如何应对工程实践上的问题。
- 网页爬虫中的URL去重:哈希 ==> 空间优化 ==> 位图 ==> 值空间很大,继续优化 ==> 布隆过滤器。将较大的值空间映射到较小的值空间会引起冲突,可以使用K 个哈希函数,对同一个数字进行求哈希值,那会得到 K 个不同的哈希值,用 K 个二进制位,来表示一个数字的存在。PS:与链表法类似,K个哈希函数也是解决冲突的一种方式。
- 如何利用朴素贝叶斯算法过滤垃圾短信?可以认为数学原理的工程化运用了,
P(A|B)=P(A) * P(B/A) / P(B)这个公式在数学上平淡无奇,但工程价值在于:实践中右侧数据比 左侧数据更容易获得。 - 向量空间:如何实现一个简单的音乐推荐系统?字符串的距离-相似度 ==> 两个人对歌曲爱好的相似度。
- 思考如何将常用算法并行化,很多时候简单的并行化优化 就超过了算法优化带来的性能提升。
- 为什么做搜索的公司技术都很牛?为什么要学数据结构与算法?为什么业务程序猿感觉数据结构与算法没用?剖析搜索引擎背后的经典数据结构和算法 光一个最最简单的搜索引擎涉及的数据结构和算法就有:图、散列表、Trie 树、布隆过滤器、单模式字符串匹配算法、AC 自动机、广度优先遍历、归并排序等。
很多时候,放弃最优解,寻找次优解,可以极大的降低工程实现上的复杂度。
小结
一个很深的体会是:算法可以很多样,但算法是逐步优化出来的,并且优化思路是一脉相承的。
几乎所有的字符串匹配算法,都是暴力匹配算法的优化,都符合“当遇到不匹配的字符时,将模式串往后滑动一下再进行匹配”,优化的点在于:如何发现规律,多滑动几位。几乎所有的“多阶段决策最优解”算法 都是回溯法的优化,秉承一个思路:先找一个路径,不行就再找下一个。优化的点在于:如何发现规律, 进而优化向下搜索和向上回溯过程。
类似的,数据结构也是优化出来的,java的Hashmap 是“数组+链表”的存储结构,而链表的结构从一般链表演化为红黑树。其实链表部分用什么结构都无所谓,红黑树、跳表都可以。“数组+链表”并不是一个专门结构,“数组+xx” 、“xx+xx”可以随意,本质都是一个二维信息的逻辑结构。
所以,数据结构和算法 都是优化出来的,其在高层抽象上都是一致的。
选择数据库与算法的取舍:
- 时间、空间复杂度不能跟性能划等号
- 抛开数据规模谈数据结构和算法都是“耍流氓”
- 结合数据特征和访问方式来选择数据结构。最考验能力的并不是数据结构和算法本身,而是对问题需求的挖掘、抽象、建模。如何将一个背景复杂、开放的问题,通过细致的观察、调研、假设,理清楚要处理数据的特征与访问方式,这才是解决问题的重点。为什么很多业务程序猿觉得数据结构和算法没用?提到:具体的数据结构是次要的,对目标问题的可利用的属性、数学模型的特殊属性、以及运行系统的物理属性保持高度敏感才是关键。 兵法上说:以正合,以奇胜。对应到算法领域就是,靠暴力算法正面维持,寻找对手的弱点,奇袭、迂回、突击战“以奇胜”。
- 区别对待 IO 密集、内存密集和计算密集。如果你要处理的数据存储在磁盘,比如数据库中。那代码的性能瓶颈可能在磁盘 IO,而并非算法本身。需要合理地选择数据存储格式和存取方式,减少磁盘 IO 的次数。字符串比较操作,实际上就是内存密集型的,需要考虑是否能减少数据的读取量,数据是否在内存中连续存储,是否能利用 CPU 缓存预读。
- 善用语言提供的类,避免重复造轮子
- 千万不要漫无目的地过度优化
总之,数据结构和算法的选择不只是技术问题,还要考虑工程上隐含的要求和约束。
在实际的软件开发中,业务纷繁复杂,功能千变万化,但是,万变不离其宗。如果抛开这些业务和功能的外壳,其实它们的本质都可以抽象为“对数据的存储和计算”。对应到数据结构和算法中,那“存储”需要的就是数据结构,“计算”需要的就是算法。对于存储的需求,功能上无外乎增删改查。这其实并不复杂。但是,一旦存储的数据很多,那性能就成了这些系统要关注的重点,特别是在一些跟存储相关的基础系统(比如 MySQL 数据库、分布式文件系统等)、中间件(比如消息中间件 RocketMQ 等)中。PS:任何一个系统的设计都有功能和性能 两个部分,识别系统模块属于哪个部分,有助于简化对系统的认识。
个人微信订阅号
