简介
笔者最近在和同事准备校招题的时候,有一道涉及到回溯的编程题,发现自己也不会,看了答案也没什么感觉,因此收集材料整理下。
本文涉及到两道题目:
-
利用字符‘a’、‘b’ 、 ‘c’ 、‘d’ 、‘e’ 、‘f’、‘g’生成并输出所有可能的字符串(但字符不可重复使用,输出顺序无要求),比如: “a”、“b”、“c”、“d”、“e”、“f”、“g”、“ab”、“ba”、“ac”、“ca”
-
集合A的幂集是由集合A的所有子集所组成的的集合,如:
A=1,2,3,则A的幂集P(A)={1,2,3},{1,2},{1,3},{1},{2,3},{2},{3},{ },求一个集合的幂集就是求一个集合的所有的子集。来自回溯法求幂集
两个问题基本一样,主要是回溯法求幂集 对回溯法的一些思路表述的比较精彩。下文会混用两个问题。
重新理解递归
写递归函数的正确思维方法基本要点:
- 看到一个递归实现, 我们总是难免陷入不停的回溯验证之中(把变量的变化依次写出来), 因为回溯就像反过来思考迭代, 这是我们习惯的思维方式, 但是其实无益于理解。数学归纳法才是理解的递归的方式,函数式编程也有这么点意思。
回溯法
基本要点:回溯法是设计递归过程的一种重要的方法,它的求解过实质上是一个先序遍历一棵“状态树”的过程,只是这棵树不是遍历前预先建立的,而是隐含在遍历过程中的。
这句话,体现在数据结构上(存储状态树)就是,正常使用一维数组存储一棵二叉树套路是
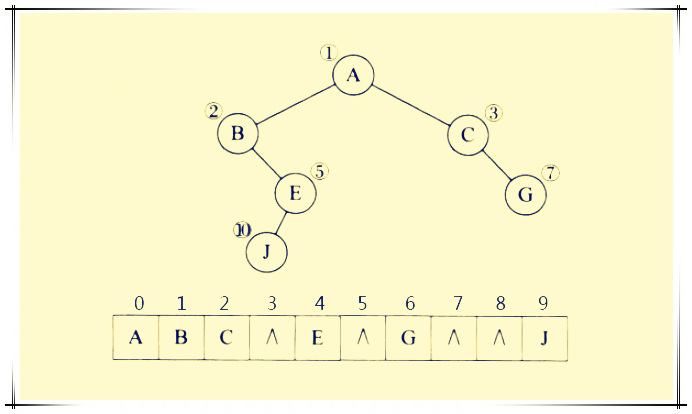
而一般未加约定的数组,只能存储树的某一分支的所有数据。在递归树的过程中,数组不断变化。当我们将一个问题抽象为一个棵树,到叶子/非叶子节点的路径是一个解决方案时,递归是罗列出所有解决的方案的代码手段。注意,通常是一个路径,而不是叶子节点代表一个解。
这也回到了算法的本质:构造解空间,从中选出符合条件的解。
求子集
其中“ab”=“ba”
迭代法:
for(i=0;i<len;i++){
for(j=i;j<len;j++){
print(str,i,j);
}
}
位图法
设原集合为<a,b,c,d>,数组A的某次“加一”后的状态为[1,0,1,1],则本次输出的子集为<a,c,d>
那么从数字0 ==> [0,0,0,0],每次加1 ==> [0,0,0,1],一直到[1,1,1,1]
回溯法
此处参考回溯法求幂集对回溯法的描述。
幂集中的每个元素是一个集合,它或是空集,或含集合A中一个元素,或含集合A中两个元素…… 或等于集合A。反之,从集合A 的每个元素来看,它只有两种状态:它或属幂集的无素集,或不属幂集的元素集。则求幂集p(A)的元素的过程可看成是依次对集合A中元素进行“取”或“舍”的过程,并且可以用一棵二叉树来表示过程中幂集元素的状态变化过程,树中的根结点表示幂集元素的初始状态(空集);叶子结点表示它的终结状态,而第i层的分支结点,则表示已对集合A中前i-1个元素进行了取舍处理的当前状态(左分支表示取,右分支表示舍 )。因此求幂集元素的过程即为先序遍历这棵状态树的过程
public class B {
private String str = "abc";
private int[] x = new int[3];
private void print(int[] x) {
for (int i = 0; i < x.length; i++) {
if (x[i] == 1) {
System.out.print(str.charAt(i));
}
}
System.out.println();
}
public void backtrack(int i) {
/*
x[i] 本质也是个位图,等x[i]从0到len赋值完毕,即可根据位图打印字符串
*/
if (i >= str.length()) {
// 到达叶子节点
print(x);
} else {
for (int isChoose = 0; isChoose <= 1; isChoose++) {
x[i] = isChoose;
backtrack(i + 1);
}
/*相当于
x[i] = 0;
backtrack(i + 1);
x[i] = 1;
backtrack(i + 1);
这就有了二叉树分叉的效果
*/
}
}
public static void main(String[] args) {
new B().backtrack(0);
}
}
对于代码:
backtrack{
if (i >= str.length()) {
print(x);
}else{
x[i] = 0;
backtrack(i + 1);
x[i] = 1;
backtrack(i + 1);
}
}
对于局部变量,递归函数每次运行时,都是全新的。如果递归函数操作全局数组,则在递归的过程中,就天然的有了二叉树分叉的效果。 此处,{x0 ==> x2 ==> x2} 代表一条路径。
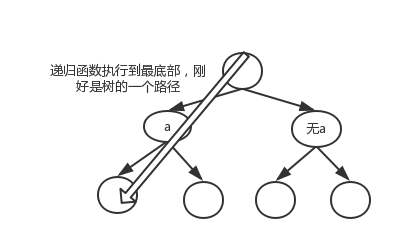
可以推断,表示一个三叉树的先序遍历,需要在同一层调用三次递归方法,此时x[i]就是另外的含义了。
x[i] = 0;
backtrack(i + 1);
x[i] = 1;
backtrack(i + 1);
x[i] = 2;
backtrack(i + 1);
回溯时,还有另外一种实现思路,即使用xc[i]直接存储子集
private String str = "abc";
private char[] xc = new char[3];
public void backtrack(int i) {
System.out.println(new String(xc));
if (i >= str.length()) {
return;
} else {
xc[i] = str.charAt(i);
backtrack(i + 1);
xc[i] = 0;
backtrack(i + 1);
}
}
全排列
用树描述一下所有解空间,注意,分叉的数目是逐渐减少的。
逐步构建全排列
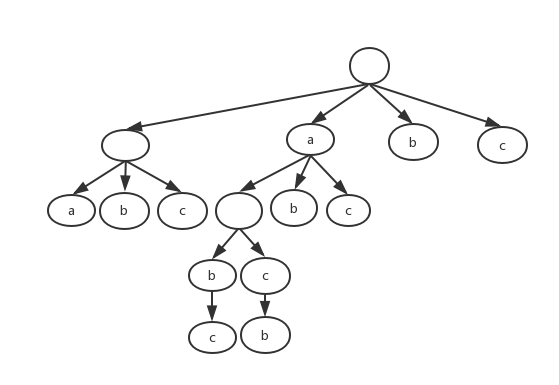
代码如下
private String str = "abc";
private int[] x = new int[3];
private char[] xc = new char[3];
public void backtrack(int i) {
if (i >= str.length()) {
System.out.println(new String(xc));
} else {
for (int t = 0; t < str.length(); t++) {
// 如果str.charAt(t)还未被选入到xc中
if (x[t] == 0) {
x[t] = 1;
xc[i] = str.charAt(t);
backtrack(i + 1);
x[t] = 0;
xc[i] = 0;
}
}
}
}
此处x[t]即表示特定位置的字符是否已被加入到xc,如已经加入,则不递归。因此循环每次都是从0开始,通过if 判断也达到减少分支的效果。此处x数组的最终结果都是111,{000 ==> 100 ==> 110 ==> 111} 代表一条路径。
全排列的另一种解法
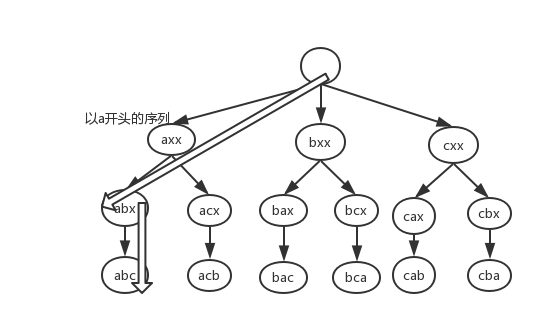
private String str = "abc";
public void backtrack(String str, int i) {
if (i >= str.length()) {
System.out.println(str);
} else {
// 每个字符都有当第一个字符的机会,所以n个字符开n个分叉,然后分叉逐渐减少
for (int t = i; t < str.length(); t++) {
str = swap(str, t, i);
backtrack(str,i + 1);
str = swap(str, i, t);
}
}
}
此处,swap函数用以实现每个字符当字符串首字符的效果,达到该效果也可以采用其它函数,比如
// 将index 字符作为首字符
private String firstChar(String str, int index) {
StringBuilder sb = new StringBuilder(str);
sb.deleteCharAt(index);
sb.insert(0, str.charAt(index));
return sb.toString();
}
// 将首字符放在index位置,作为firstChar的反操作
private String _firstChar(String str, int index) {
StringBuilder sb = new StringBuilder(str);
sb.deleteCharAt(0);
sb.insert(index, str.charAt(0));
return sb.toString();
}
public void backtrack(String str, int i) {
if (i >= str.length()) {
System.out.println(str);
} else {
for (int t = i; t < str.length(); t++) {
str = firstChar(str, t);
backtrack(str, i + 1);
str = _firstChar(str, t);
}
}
}
只是需要firstChar和_firstChar两个函数,不如swap来得简洁。但一简洁,导致很多博客通过交换来理解全排列,增加的理解的难度。
子集 + 全排列
即对于子集“ab”!=“ba”
第一感觉的方法:先求所有子集,再对所有子集全排列。
此外,对本文的全排列方法进行调整,即可在递归全排列的过程中,顺带输出子集。
public void backtrack(int i) {
// 全排列过程中,此时xc还未构造完毕,相当于输出了子集
System.out.println(new String(xc));
if (i >= str.length()) {
return;
} else {
for (int t = 0; t < str.length(); t++) {
if (x[t] == 0) {
x[t] = 1;
xc[i] = str.charAt(t);
backtrack(i + 1);
x[t] = 0;
xc[i] = 0;
}
}
}
}
小结
计算机并没有“大招”,关键是思维不要乱窜
直接看回溯的代码,通常会感觉莫名其妙,也非常容易遗忘。对于刷题的同学来说,则是非常大的记忆负担。其中的关节,便是建立一系列的抽象,来屏蔽一些实现细节。假设一个复杂系统要三层抽象,每一层都需要一些复杂算法。那么第三层的细节与第二层的细节一下子涌入脑海,人就容易懵逼。