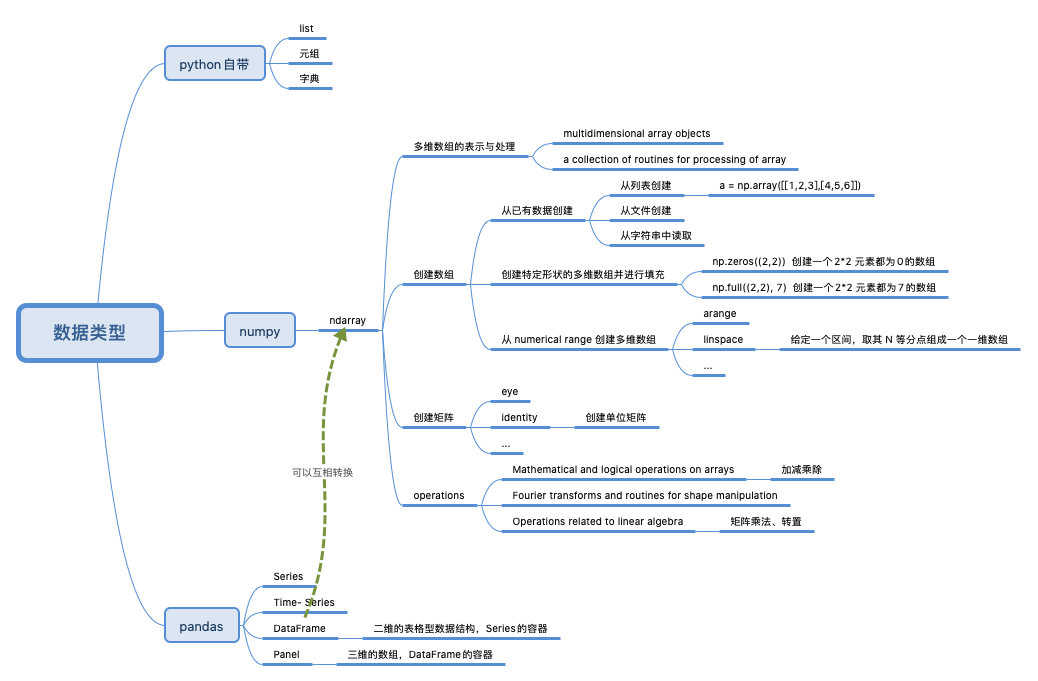
简介
《极客时间》重学线性代数
代数是构造一系列对象和一系列操作这些对象的规则。我们类比来看,线性代数其实就是向量,以及操作这些向量的规则。
向量,也叫欧几里得向量(Euclidean Vector),其实就是能够互相相加、被标量乘的特殊对象,结果也是向量。
- 几何向量是有向线段,两个几何向量能够相加也能被一个标量乘。
- 多项式其实也是向量。两个多项式能够相加,它也能够被标量乘,结果也是多项式。
- 矩阵的一行或一列也是向量。
- 矢量图、音频信号也是向量。
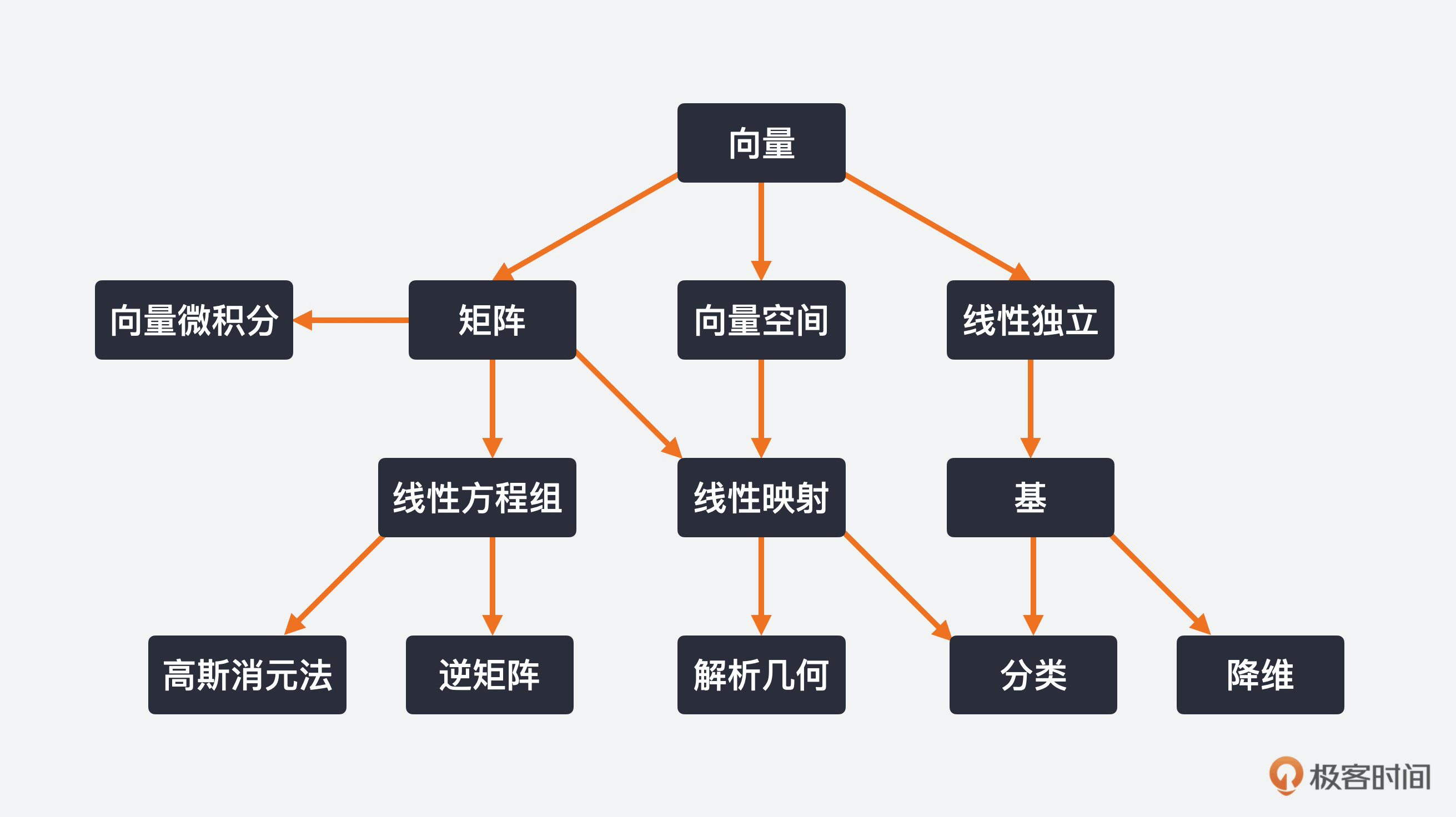
矩阵
第一个例子是计算旅游团人数。假设,一个旅游团由孩子和大人组成,去程时他们一起坐大巴,每个孩子的票价 3 元,大人票价 3.2 元,总共花费 118.4 元。回程时一起坐火车,每个孩子的票价 3.5 元,大人票价 3.6 元,总共花费 135.2 元。请问这个旅游团中有多少孩子和大人?假设小孩人数为 x1,大人人数为 x2,于是我们得到了一个方程组:
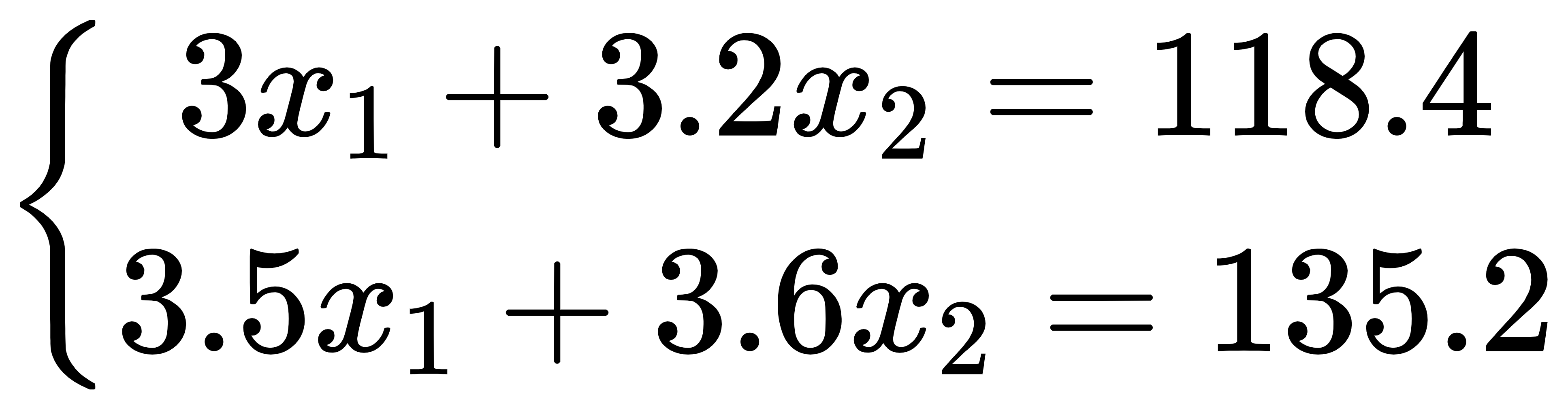
线性方程组的几何表达:在一个只有两个变量 x1,x2 的线性方程组中,我们定义一个 x1,x2 平面。在这个平面中,每个线性方程都表达了一条直线。由于线性方程组的唯一解必须同时满足所有的等式,所以,线性方程组的唯一解其实就是线段的相交点,无穷解就是两线重合,而无解的情况,也就是两条线平行。
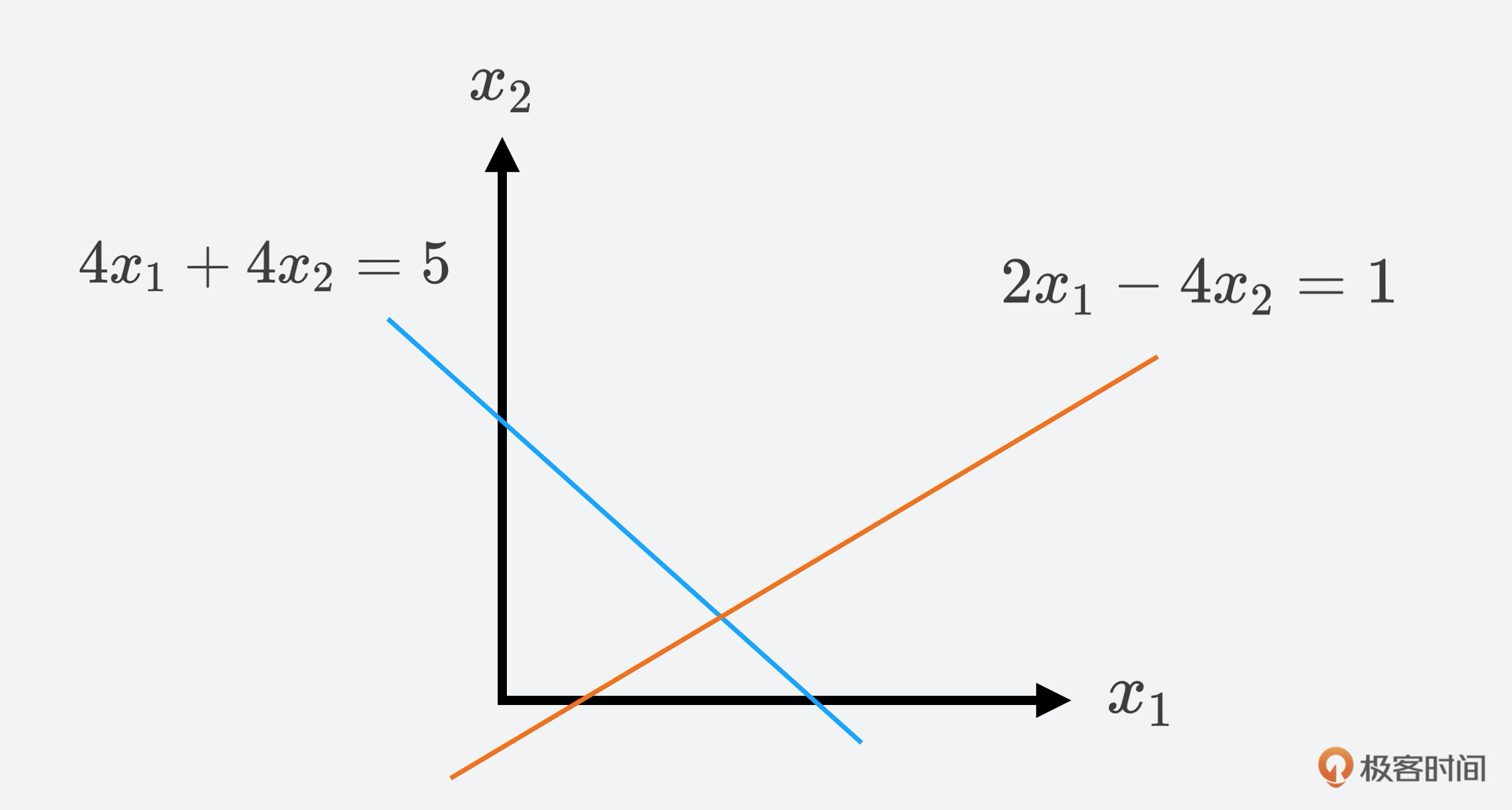
英国数学家 Arthur Cayley 被公认为矩阵论的创立人,他提出的矩阵概念可能来自于行列式。但我相信另一种说法,提出矩阵是为了更简单地表达线性方程组,也就是说,矩阵是线性方程组的另一种表达。

矩阵法求解:要解 X,我们就要先计算 A 的逆矩阵 $A^{-1}$
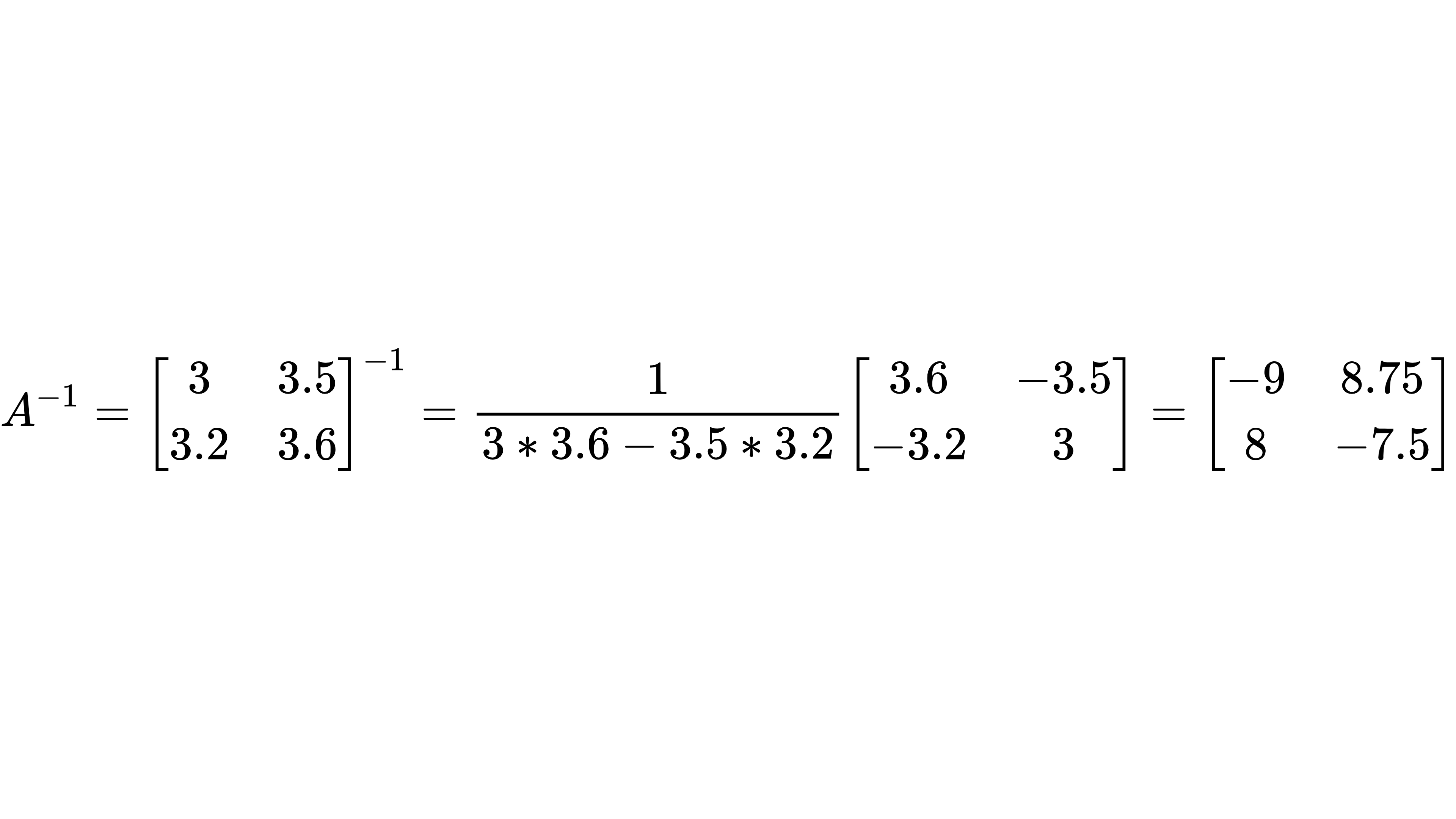
接下来再计算 $X=BA^{−1}$
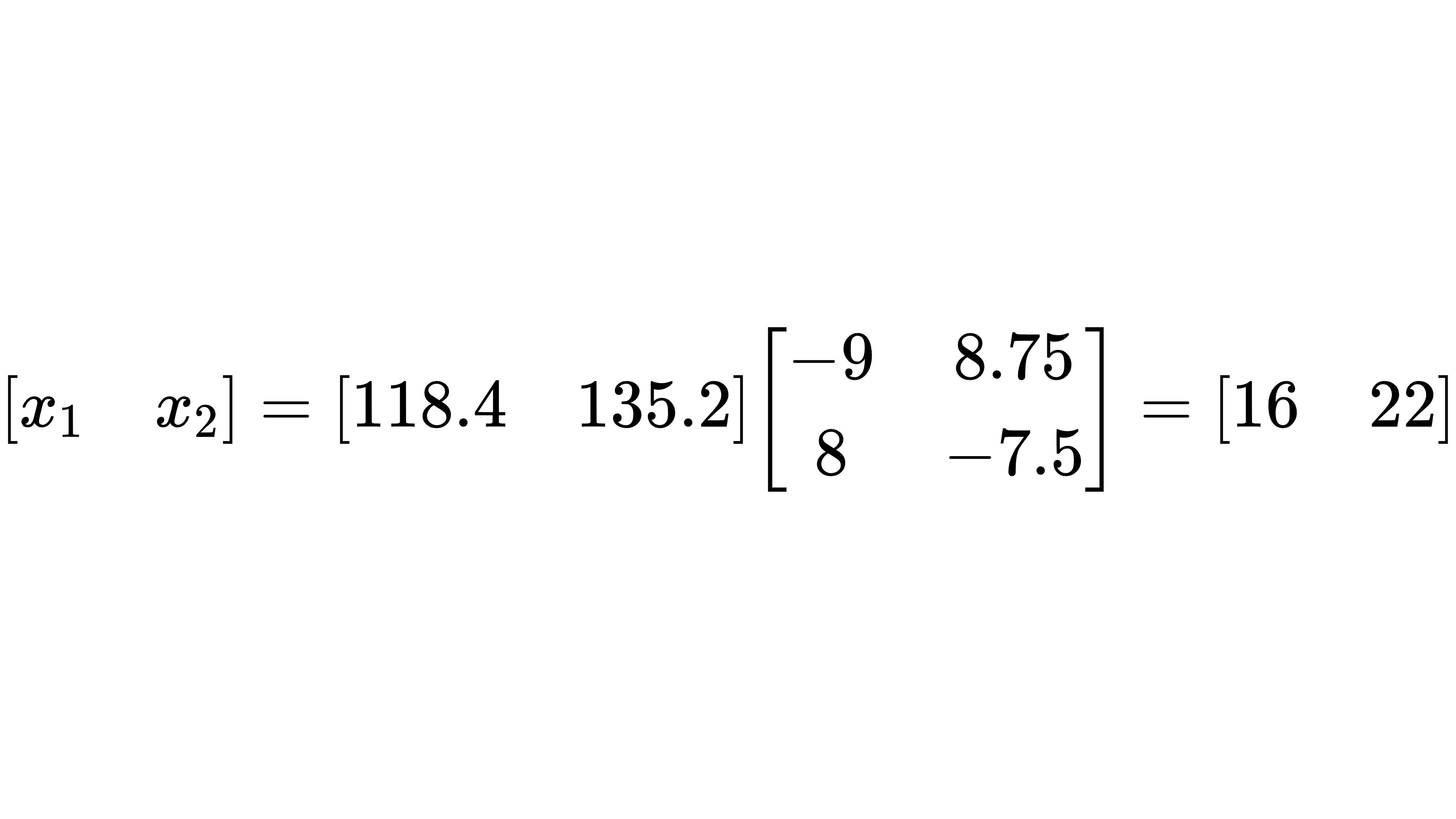
简单的线性方程组,我们当然可以运用初中学过的知识来求解,那复杂的呢?硬来几乎是不可能的了。线性方程组是能够通过矩阵或向量来表达的,可以使用高斯消元法来解线性方程(直接法),面对百万、千万级别的变量时,还需要间接法/迭代法。
以线性方程组 Ax=b 为例。在这里我们分解 A,使得 A=S−T,代入等式后得出:Sx=Tx+b,按这样的方式持续下去,通过迭代的方式来解 Sx。这就类似于把复杂问题层层分解和简化,最终使得这个迭代等式成立:$Sx_{k+1}=Tx_{k}+b$,更具体一点来说,我们其实是从 x0 开始,解 $Sx_{1}=Tx_{0}+b$。然后,继续解 $Sx_2=Tx_{1}+b$,一直到 $x_{k+1}$ 非常接近 $x_{k}$ 时,由于线性方程组的复杂程度不同,这个过程经历几百次的迭代都是有可能的。所以,迭代法的目标就是比消元法更快速地逼近真实解。那么究竟应该如何快速地逼近真实解呢?这里,A=S−T,A 的分解成了关键,也就是说 A 的分解目标是每步的运算速度和收敛速度都要快。S 选择的几种常见方法:雅可比方法;高斯 - 赛德尔方法;ILU 方法。
从计算机科学的角度来说,使用矩阵的运算效率实在是高太多了,因为它可以利用计算机的并行能力,甚至在一些迭代法中,还能实现分布式并行计算。大密度线性方程组的计算已经成为了世界上最快计算机的测试标准。
numpy
NumPy是Python中用于数据分析、机器学习、科学计算的重要软件包。它极大地简化了向量和矩阵的操作及处理。《用python实现深度学习框架》用python 和numpy 实现了一个深度学习框架MatrixSlow
- 支持计算图的搭建、前向、反向传播
- 支持多种不同类型的节点,包括矩阵乘法、加法、数乘、卷积、池化等,还有若干激活函数和损失函数。比如向量操作pytorch 跟numpy 函数命名都几乎一样
- 提供了一些辅助类和工具函数,例如构造全连接层、卷积层和池化层的函数、各种优化器类、单机和分布式训练器类等,为搭建和训练模型提供便利
多维数组的属性
- ndim, 数组维度(或轴)的个数
- shape, 表示数组的维度或形状
- size, 也就是数组元素的总数
- type , 数组所属的数据类型
- axis, 数组的轴, 即数组的维度,它是从 0 开始的。对于我们这个二维数组来说,有两个轴,分别是代表行的 0 轴与代表列的 1 轴。比如沿着 0轴求和
np.sum(interest_score, axis=0)
数组访问
import numpy as np
b = np.array([[1,2,3],[4,5,6],[7,8,9],[10,11,12]],dtype=int)
c = b[0,1] #1行 第二个单元元素
# 输出: 2
d = b[:,1] #所有行 第二个单元元素
# 输出: [ 2 5 8 11]
e = b[1,:] #2行 所有单元元素
# 输出: [4 5 6]
f = b[1,1:] #2行 第2个单元开始以后所有元素
# 输出: [5 6]
g = b[1,:2] #2行 第1个单元开始到索引为2以前的所有元素
pytorch 张量/Tensor
numpy作为一个科学计算库,并不包含:计算图,尝试学习,梯度等等功能
the deep learning machine is a rather complex mathematical function mapping inputs to an output. To facilitate expressing this function, PyTorch provides a core data structure, the tensor, which is a multidimensional array that shares many similarities with NumPy arrays. Around that foundation, PyTorch comes with features to perform accelerated mathematical operations on dedicated hardware, which makes it convenient to design neural network architectures and train them on individual machines or parallel computing resources.
在深度学习过程中最多使用$5$个维度的张量,张量的维度(dimension)通常叫作轴(axis)
- 标量(0维张量)
- 向量(1维度张量)
- 矩阵(2维张量)
- 3维张量,最常见的三维张量就是图片,例如$[224, 224, 3]$
- 4维张量,4维张量最常见的例子就是批图像,加载一批 $[64, 224, 224, 3] 的图片,其中 $64$ 表示批尺寸,$[224, 224, 3]$ 表示图片的尺寸。
- 5维张量,使用5维度张量的例子是视频数据。视频数据可以划分为片段,一个片段又包含很多张图片。例如,$[32, 30, 224, 224, 3]$ 表示有 $32$ 个视频片段,每个视频片段包含 $30$ 张图片,每张图片的尺寸为 $[224, 224, 3]$。
本质上来说,PyTorch 是一个处理张量的库。能计算梯度、指定设备等是 Tensor 相对numpy ndarray 特有的
- Tensor的结构操作包括:创建张量,查看属性,修改形状,指定设备,数据转换, 索引切片,广播机制(不同形状的张量相加),元素操作,归并操作;
- Tensor的数学运算包括:标量运算,向量运算,矩阵操作,比较操作。
张量有很多属性,下面我们看看常用的属性有哪些?
- tensor.shape,tensor.size(): 返回张量的形状;
- tensor.ndim:查看张量的维度;
- tensor.dtype,tensor.type():查看张量的数据类型;
- tensor.is_cuda:查看张量是否在GPU上;
- tensor.grad:查看张量的梯度;
- grad_fn: 包含着创建该张量的运算的导数信息。在反向传播过程中,通过传入后一层的神经网络的梯度,该函数会计算出参与运算的所有张量的梯度。grad_fn本身也携带着计算图的信息,该方法本身有一个next_functions属性,包含连接该张量的其他张量的grad_fn。通过不断反向传播回溯中间张量的计算节点,可以得到所有张量的梯度。
- tensor.requires_grad:查看张量是否可微。
- tensor.device: 获取张量所在的设备
涉及单个张量的函数运算,例如 对张量做四则运算、线性变换和激活、缩并、沿着某个维度求和、数据在设备之间移动。可以由张量自带的方法实现,也可以由torch包中的一些函数实现
- 一元运算(Unary),如sqrt、square、exp、abs等。
- 二元运算(Binary),如add,sub,mul,div等
- 选择运算(Selection),即if / else条件运算
- 归纳运算(Reduce),如reduce_sum, reduce_mean等
- 几何运算(Geometry),如reshape,slice,shuffle,chip,reverse,pad,concatenate,extract_patches,extract_image_patches等
- 张量积(Contract)和卷积运算(Convolve)是重点运算,后续会详细讲解。
用张量验证 链式法则
y1 = x * w1 + b1
y2 = y1 * w2 + b2
dy2_dy1 = autograd.grad(y2,[y1],retain_graph=True)[0]
dy1_dw1 = autograd.grad(y1,[w1],retain_graph=True)[0]
dy2_dw1 = autograd.grad(y2,[w1],retain_graph=True)[0]
可以对比下 dy2_dy1 * dy1_dw1 和 dy2_dw1 的值
用张量运算表示 多层感知机
Multilayer perceptron
x = torch.randn(3,1,requires_grad=True)
print(x)
y = x.pow(2).sum()
y.backward()
print(x.grad)
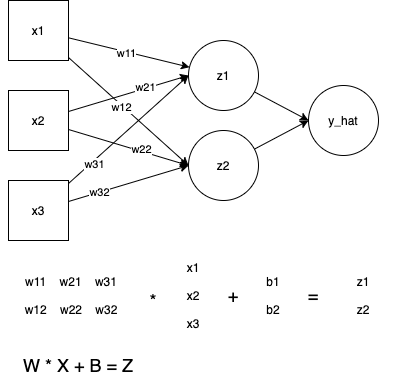
输入向量 乘以 权重矩阵 得到输出向量,然后我们可以得到权重矩阵的 梯度。 如果演示 矩阵运算 $Y = X^2$ 观察X梯度矩阵 与 矩阵X的 值(前者是后者的2倍)会更明显一些。
import torch
w1 = torch.randn(2,3,requires_grad=True)
print(w1)
x = torch.randn(3,1,requires_grad=True)
b1 = torch.randn(2,1,requires_grad=True)
w2 = torch.randn(2,2,requires_grad=True)
b2 = torch.randn(1,1,requires_grad=True)
z = w1 @ x + b1
y = (w2 @ z + b2).sum()
print(y)
y.backward()
print(w1.grad)
## 输出
tensor([[-0.1884, 0.2570, -0.7091],
[ 0.3521, -0.1305, -3.2695]], requires_grad=True)
tensor(0.4844, grad_fn=<SumBackward0>)
tensor([[-0.1294, 0.0312, -0.0236],
[-0.9929, 0.2397, -0.1814]])
《李沐的深度学习课》 有一点非常好,就是针对线性回归/softmax回归/感知机 都提供了一个 基于numpy 的实现以及pytorch 的简单实现。
- 标量运算:(标量之间)加减乘除,长度,求导(导数是切线的斜率)
- 向量运算:(标量向量之间,向量之间)加减乘除, 长度, 求导(也就是梯度,跟等高线正交)
- 矩阵运算:(标量矩阵之间,向量矩阵之间,矩阵矩阵之间)加减乘, 转置, 求导

x = torch.tensor([[1.0,2,3],[4,5,6]],requires_grad=True)
print(x)
y = x + 1
print(y)
z = 2 * y * y
print(z)
j = torch.mean(z)
print(j)
j.backward()
print(x.grad)
用张量运算表示机器学习过程
在机器学习模型是,j 就是损失函数。x 是 <w,b> (存疑 ),机器学习中,<w,b> 是参数或变量,样本数据数据是为了计算 loss值。
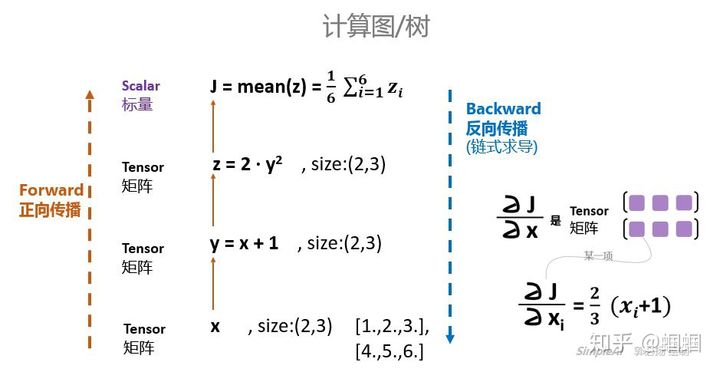
\(\frac{dj}{dz_i}=\frac{1}{6}\) \(\frac{dz}{dy}=4y\) \(\frac{dy}{dx}=1\) \(\frac{dj}{dx_i}=\frac{1}{6} * 4 * (x_i+1) = \frac{2}{3}(x_i+1)\)
线性模型可以看做是单层(带权重的层只有1层)神经网络
| 使用pytorch 手动实现线性模型 | 使用pytorch直接配置线性模型 |
// Initialize Model Parameters
w = torch.zeros(size=(num_inputs, 1)).normal_(std=0.01)
b = torch.zeros(size=(1,))
w.requires_grad_(True)
b.requires_grad_(True)
// Define the Model
def linreg(X, w, b):
return torch.matmul(X, w) + b
// Define the Loss Function
def squared_loss(y_hat, y):
return (y_hat - y.reshape(y_hat.shape)) ** 2 / 2
// Define the Optimization Algorithm
def sgd(params, lr, batch_size):
for param in params:
param.data.sub_(lr*param.grad/batch_size)
param.grad.data.zero_()
// Training
lr = 0.03 # Learning rate
num_epochs = 3 # Number of iterations
net = linreg # Our fancy linear model
loss = squared_loss # 0.5 (y-y')^2
for epoch in range(num_epochs):
# Assuming the number of examples can be divided by the batch size, all
# the examples in the training data set are used once in one epoch
# iteration. The features and tags of mini-batch examples are given by X
# and y respectively
for X, y in data_iter(batch_size, features, labels):
l = loss(net(X, w, b), y) # Minibatch loss in X and y
l.mean().backward() # Compute gradient on l with respect to [w,b]
sgd([w, b], lr, batch_size) # Update parameters using their gradient
with torch.no_grad():
train_l = loss(net(features, w, b), labels)
print('epoch %d, loss %f' % (epoch + 1, train_l.mean().numpy()))
// print training result
print('Error in estimating w', true_w - w.reshape(true_w.shape))
print('Error in estimating b', true_b - b)
|
// Define the Model
net = LinearRegressionModel()
// Initialize Model Parameters
net.layer1.weight.data=torch.Tensor(np.random.normal(size=(1,2),scale=0.01,loc=0))
net.layer1.bias.data=torch.Tensor([0])
// Define the Loss Function
loss = torch.nn.MSELoss(reduction = "sum")
// Define the Optimization Algorithm
trainer = torch.optim.SGD(net.parameters(), lr = 0.03)
// Training
num_epochs = 3
for epoch in range(num_epochs):
for X,y in data_iter:
l=loss(net(X) ,y)
trainer.zero_grad()
l.backward()
trainer.step()
l_epoch = loss(net(features), labels)
print('epoch {}, loss {}'.format(epoch+1, l_epoch))
// print training result
w = list(net.parameters())[0][0]
print('Error in estimating w', true_w.reshape(w.shape) - w)
b = list(net.parameters())[1][0]
print('Error in estimating b', true_b - b)
|
各种模型纵有千万种变化,但是依然离不开以下几步:
- 模型结构设计:例如,机器学习中回归算法、SVM 等,深度学习中的 VGG、ResNet、SENet 等各种网络结构,再或者你自己设计的自定义模型结构。
- 给定损失函数:损失函数衡量的是当前模型预测结果与真实标签之间的差距。
- 给定优化方法:与损失函数搭配,更新模型中的参数。
这里面变化最多的就是模型结构了,这一点除了多读读论文,看看相关博客来扩充知识面之外,没有什么捷径可走。然后呢,我们也不要小瞧了损失函数,不同的损失函数有不同的侧重点,当你模型训练处于瓶颈很难提升,或者解决不了现有问题的话,可以考虑考虑调整一下损失函数。
从中可以找到一点感觉,就是如果 mapreduce 让你写map和reduce 函数,那么pytorch 就只是让你设定 网络每层大小、损失函数、 优化器方法名等。
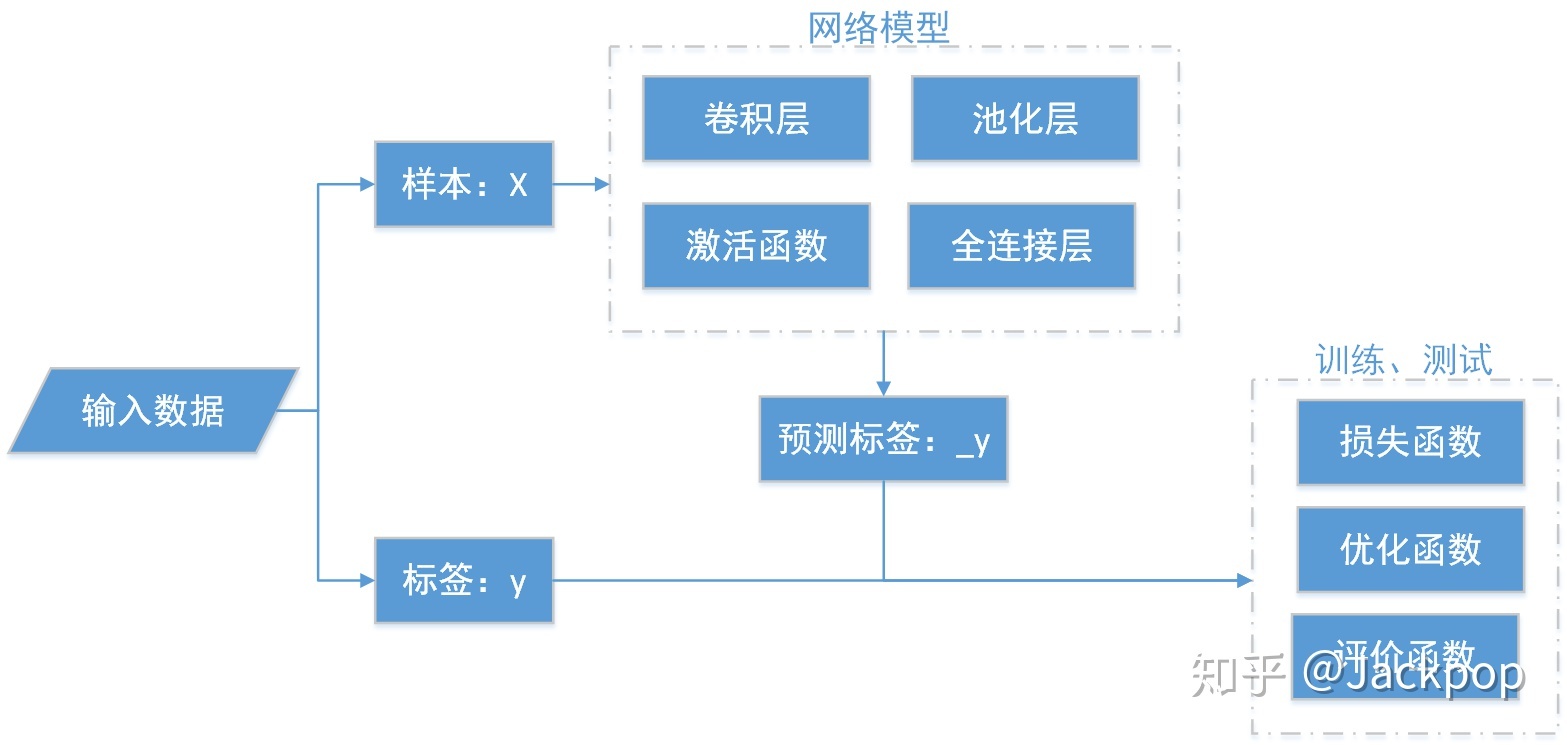
net 此处代表一层网路模型,具象化为一个tensor 计算。
def linreg(X, w, b):
return torch.matmul(X, w) + b
对于两层网络模型
W1 = xx
b1 = xx
W2 = xx
b2 = xx
def relu(X): # 定义激活函数
a = torch.zeros_like(X)
return torch.max(X,a)
def net(X): # 模型可以表示为矩阵运算
X = X.reshape((-1,num_inputs))
H = relu(X * W1 + b1)
return (H * W2 + b2)
假设一个层数为L 的多层感知机的第l 层 $H^{(l)}$ 的权重参数为 $W^{(l)}$,输出层$H^{(L)}$的权重参数为$W^{L}$。为了方便讨论,不考虑偏差函数,且设所有隐藏层的激活函数为恒等映射 $\sigma(x) = x$。 给定输入X,多层感知机的第l 层的输出$H^{(l)}=XW^{(1)}W^{(2)}…W^{(l)}$。PS:原理和矩阵运算对上了。
手动实现时,net 是一个方法,定义了预测值的计算方法,模型可以表示为矩阵运算。应该尽可能表示为矩阵运算,以提升计算效率。 pytorch nn模块定义了大量神经网络的层,loss模块定义了各种损失函数,net和 tensor 一样可以 net.to(device="cuda:1") 将数据挪到某个gpu 上。要想在某个 gpu 上做运算,需要将模型参数(net)和输入(tensor) 都挪到这个gpu 上。
用所有数据训练一遍就是一个 Epoch。但受到硬件设备的限制,训练时不会一次性的读入所有数据,而是一次读入一部分进行训练,这里的“每次”就是对应的 Step 这个概念。那每次读入的数据量就是 batch_size。训练集有1000个样本,batchsize=10,那么:训练完整个样本集需要100次iteration,1次epoch。
其它